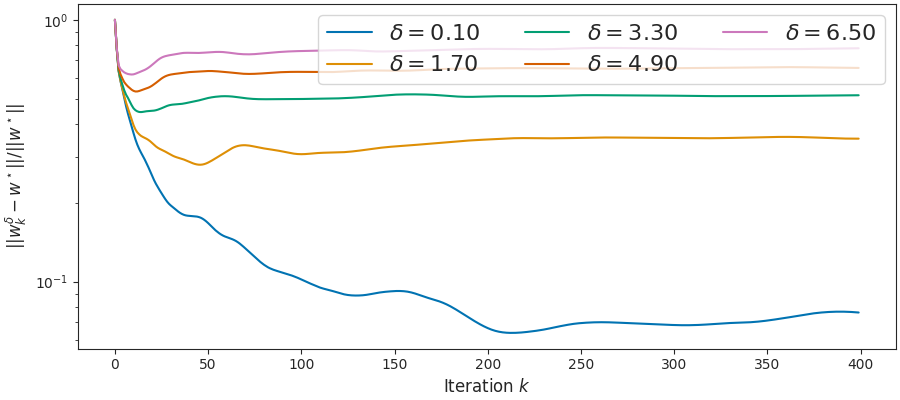
Show existence of stopping time

This is for L1 regression.

Out:

usetex mode requires TeX.
/home/circleci/.local/lib/python3.8/site-packages/sklearn/linear_model/_base.py:133: FutureWarning: The default of 'normalize' will be set to False in version 1.2 and deprecated in version 1.4.
If you wish to scale the data, use Pipeline with a StandardScaler in a preprocessing stage. To reproduce the previous behavior:

from sklearn.pipeline import make_pipeline

model = make_pipeline(StandardScaler(with_mean=False), LassoLars())

If you wish to pass a sample_weight parameter, you need to pass it as a fit parameter to each step of the pipeline as follows:

kwargs = {s[0] + '__sample_weight': sample_weight for s in model.steps}
model.fit(X, y, **kwargs)

Set parameter alpha to: original_alpha * np.sqrt(n_samples).
  warnings.warn(
0.1
1.7000000000000002
3.3000000000000003
4.9
6.5

import numpy as np
import matplotlib.pyplot as plt

from numpy.linalg import norm
from sklearn.linear_model import LassoLars
from joblib import Parallel, delayed

from iterreg.sparse import dual_primal
from iterreg.utils import make_sparse_data


from celer.plot_utils import configure_plt
configure_plt()


n, d = 200, 500
s = 75
rho = 0.2
np.random.seed(12)
X, y, w0 = make_sparse_data(
    n, d, s=s, rho=rho, snr=None, w_type="ones", normalize=True)

scal = 20 / norm(y)
y *= scal

clf = LassoLars(alpha=1e-20, fit_intercept=False)
clf.fit(X, y)
w_bp = clf.coef_


def wrapper(X, y, delta, max_iter, f_store, rep):
    print(delta, rep)
    np.random.seed(rep)
    noise = np.random.randn(y.shape[0])
    y_noise = y + delta * noise / norm(noise)
    all_w = dual_primal(
        X, y_noise, step_ratio=1, max_iter=max_iter, f_store=f_store,
        verbose=False)[-1]
    return all_w


all_wdict = dict()

max_iter = 5_000

n_deltas = 5
deltas = np.linspace(0.1, 6.5, num=n_deltas)
np.random.seed(1)
n_reps = 1
res = np.zeros([n_deltas, n_reps])

for i, delta in enumerate(deltas):
    print(delta)
    all_w_rep = np.array(Parallel(n_jobs=-1)(delayed(wrapper)(
        X, y, delta, max_iter, 1, rep)
        for rep in range(n_reps)))
    all_wdict[delta] = all_w_rep[:1].copy()

    for rep in range(n_reps):
        res[i, rep] = np.argmin(norm(all_w_rep[rep] - w_bp, axis=1))
    del all_w_rep

fig3, ax = plt.subplots(constrained_layout=True, figsize=(9, 4))
n_points = 400
for delta in deltas:
    x_plt = np.arange(len(all_wdict[delta][0]))
    y_plt = norm(all_wdict[delta][0] - w_bp, axis=1) / norm(w_bp)
    ax.semilogy(x_plt[:n_points], y_plt[:n_points],
                label=r"$\delta={:.2f}$".format(delta))

ax.set_ylabel(r'$||w^\delta_k - w^\star||/ ||w^\star||$')
ax.set_xlabel("Iteration $k$")

plt.legend(ncol=3, fontsize=16, loc='upper right')
plt.show(block=False)