Plot stopping time for low rank matrix completion

Plot the stopping time for low rank matrix completion.

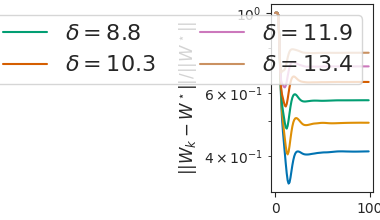
Out:

usetex mode requires TeX.
Iter 0, feasability: 8.9e+00
Iter 100, feasability: 5.0e-03
Iter 200, feasability: 9.0e-04
Iter 300, feasability: 3.0e-04
Iter 400, feasability: 1.2e-04
Iter 500, feasability: 5.8e-05
Iter 600, feasability: 3.0e-05
Iter 700, feasability: 1.5e-05
Iter 800, feasability: 8.2e-06
Iter 900, feasability: 4.4e-06
Iter 1000, feasability: 2.4e-06
Iter 1100, feasability: 1.3e-06
Iter 1200, feasability: 6.9e-07
Iter 1300, feasability: 3.8e-07
Iter 1400, feasability: 2.0e-07
Iter 1500, feasability: 1.1e-07
Iter 1600, feasability: 6.0e-08
Iter 1700, feasability: 3.3e-08
Iter 1800, feasability: 1.8e-08
Iter 1900, feasability: 9.7e-09
Feasability 9.7e-09 < 1.0e-08, exit.
Feasability of W_star : 9.70e-09
5.666666666666667
7.222222222222222
8.777777777777779
10.333333333333334
11.88888888888889
13.444444444444445

import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm
from celer.plot_utils import configure_plt

from iterreg.low_rank.solvers import dual_primal_low_rank

configure_plt()


d = 100
np.random.seed(0)
mask = np.zeros([d, d], dtype=bool)
idx = np.random.choice(d ** 2, d ** 2 // 5, replace=False)
mask.flat[idx] = True
# rank = d // 10
rank = 5
Y_true = np.random.randn(d, rank) @ np.random.randn(rank, d)
Y_true /= (norm(Y_true, ord="fro") / 20)
Y = Y_true.copy()

Y[~mask] = 0

W_star, Theta, _ = dual_primal_low_rank(
    mask, Y, max_iter=3_000, stop_crit=1e-8, f_store=100, verbose=1)

print(f"Feasability of W_star : {norm((Y - W_star)[mask]):.2e}")

n_deltas = 10
deltas = np.linspace(1, 15, num=n_deltas)

noise = np.random.randn(d, d)
distances = dict()
f_store = 1

deltas = deltas[3:-1]

for delta in deltas:
    print(delta)
    Y_delta = Y_true + delta * noise / norm(noise)
    sigma = 1 / norm(Y_delta, ord=2)

    x, theta, dist = dual_primal_low_rank(
        mask, Y_delta, max_iter=200, sigma=sigma, verbose=False,
        f_store=f_store, limit=W_star)

    distances[delta] = dist

plt.close('all')
fig1, ax = plt.subplots(1, 1, constrained_layout=True, figsize=(3.8, 2.2))
n_points = 100
for delta in deltas:
    x_plt = f_store * np.arange(len(distances[delta]))
    y_plt = distances[delta] / norm(W_star)
    ax.semilogy(x_plt[:n_points], y_plt[:n_points],
                label=r"$\delta={:.1f}$".format(delta))

paper = False
if paper:
    plt.ylabel(r'$||X_k - {X}^\star|| / ||{X}^\star||$')
    plt.xlabel("iterative regularization iteration $k$")
else:
    plt.ylabel(r'$||W_k - {W}^\star|| / ||{W}^\star||$')
    plt.legend(loc='upper right', ncol=3, fontsize=16)

plt.show(block=False)


if paper:
    fig1.savefig("low_rank_d%d.pdf" % d)