 |
GURLS++
2.0.00
C++ Implementation of GURLS Matlab Toolbox
|
 |
GURLS++
2.0.00
C++ Implementation of GURLS Matlab Toolbox
|
The main namespace of GURLS++. More...
Classes | |
| class | BadConfidenceCreation |
| BadConfidenceCreation is thrown when factory tries to generate an unknown confidence method. More... | |
| class | BadKernelCreation |
| BadKernelCreation is thrown when factory tries to generate an unknown kernel. More... | |
| class | BadNormCreation |
| BadNormCreation is thrown when factory tries to generate an unknown norm. More... | |
| class | BadOptimizerCreation |
| BadOptimizerCreation is thrown when factory tries to generate an unknown optimizer. More... | |
| class | BadParamSelectionCreation |
| BadParamSelectionCreation is thrown when factory tries to generate an unknown parameter selection method. More... | |
| class | BadPerformanceCreation |
| BadPerformanceCreation is thrown when factory tries to generate an unknown performance evaluator. More... | |
| class | BadPredictionCreation |
| BadPredictionCreation is thrown when factory tries to generate an unknown prediction method. More... | |
| class | BadPredKernelCreation |
| BadPredKernelCreation is thrown when factory tries to generate an unknown prediction kernel. More... | |
| class | BadSplitCreation |
| BadSplitCreation is thrown when factory tries to generate an unknown split method. More... | |
| class | BaseArray |
| BaseArray is the base class for all classes implementing vectors and matrices as arrays of cells. More... | |
| class | BlasUtils |
| BlasUtils is a convenience class to interface with Blas. More... | |
| class | ConfBoltzman |
| ConfBoltzman is the sub-class of Confidence that computes the probability of belonging to the highest scoring class. More... | |
| class | ConfBoltzmanGap |
| ConfBoltzmanGap is the sub-class of Confidence that computes a confidence estimation for the predicted class (i.e. More... | |
| class | ConfGap |
| ConfGap is the sub-class of Confidence that computes a confidence estimation for the predicted class. More... | |
| class | Confidence |
| Confidence is the class that computes a confidence score for the predicted labels. More... | |
| class | ConfMaxScore |
| ConfMaxScore is the sub-class of Confidence that computes a confidence estimation for the predicted class (i.e. More... | |
| class | Functor |
| class | gException |
| gException is the class designed to deal with exceptions in Gurls++ package. More... | |
| class | gMat2D |
| gMat2D implements a matrix of generic size More... | |
| class | GPRWrapper |
| GPRWrapper is the sub-class of GurlsWrapper that implements ... More... | |
| class | GURLS |
| GURLS is the class that implements a GURLS process. More... | |
| class | GurlsOption |
| GurlsOption is an abstraction of a generic `option', which is widely used within the GURLS++ package to store either numeric parameters necessary to configure specific algorigms or sequences of strings holding the names of the specific procedures that have to be performed. More... | |
| class | GurlsOptionsList |
| GurlsOptionsList is an option containing a list of options mapped by name. More... | |
| class | GurlsWrapper |
| GurlsWrapper is the base class for all gurls++ wrappers. More... | |
| class | gVec |
| gVec implements a vector of generic length More... | |
| class | ICholWrapper |
| class | Kernel |
| Kernel is the class that computes the kernel matrix. More... | |
| class | KernelChisquared |
| KernelChisquared is the sub-class of Kernel that builds the kernel matrix for a chi-squared model. More... | |
| class | KernelLinear |
| KernelLinear is the sub-class of Kernel that builds the kernel matrix for a linear model. More... | |
| class | KernelRBF |
| KernelRBF is the sub-class of Kernel that builds the Gaussian kernel matrix. More... | |
| class | KernelRLSWrapper |
| KernelRLSWrapper is the sub-class of GurlsWrapper that implements Regularized Least Squares with a possibly non-linear model by resorting to kernel methods. More... | |
| class | KernelWrapper |
| KernelWrapper is the base class for all gurls++ wrappers. More... | |
| class | LtCompare |
| Auxiliary class performing floating point comparison used for std routines. More... | |
| class | Max |
Computes the largest element in a vector v of lenght n. More... | |
| class | Mean |
Computes the mean value of a vector v of lenght n. More... | |
| class | Median |
Computes the median value of a vector v of lenght n. More... | |
| class | Min |
Computes the smallest element in a vector v of lenght n. More... | |
| class | Norm |
| Norm is a class that spherifies the data. More... | |
| class | NormL2 |
| NormL2 is the sub-class of Norm that spheriphies the data according to the l2 norm. More... | |
| class | NormTestZScore |
| NormTestZScore is the sub-class of Norm that spheriphies the data according to the statistics cmoputed on the training set. More... | |
| class | NormZScore |
| NormZScore is the sub-class of Norm that centers and rescales the input data matrix X. More... | |
| class | NystromWrapper |
| NystromWrapper is the sub-class of GurlsWrapper that allows to train a possibly non linear model for large data sets, for which the complete nxn kernel matrix may not fit into RAM. More... | |
| class | OptArray |
| Optarray is an option containing an indexed array of options. More... | |
| class | OptFunction |
| OptFunction is an option representing a pointer to a generic function T (*function)(T* , int) operating over an array of floating point numbers. More... | |
| class | Optimizer |
| Optimizer is a class that implements a Regularized Least Square algorithm. More... | |
| class | OptMatrix |
| OptMatrix is an option containing a matrix. More... | |
| class | OptMatrixBase |
| OptMatrixBase is the base class for all options containing matrices. More... | |
| class | OptNumber |
| OptNumber is an option containing a double precision floating point number. More... | |
| class | OptNumberList |
| OptNumberList is an option containing a list of double precision floating point numbers. More... | |
| class | OptProcess |
| OptProcess is an option containing a sequence of actions that form a Gurls process. More... | |
| class | OptString |
| OptString is an option containing a generic string. More... | |
| class | OptStringList |
| OptStringList is an option containing a list of strings. More... | |
| class | OptTaskSequence |
| OptTaskSequence is an option containing a sequence of task that forms a pipeline. More... | |
| class | ParamSelCalibrateSGD |
| ParamselCalibrateSGD is the sub-class of ParamSelection that implements parameter selection for pegasos. More... | |
| class | ParamSelection |
| ParamSelection is the class that implements parameter selection. More... | |
| class | ParamSelFixLambda |
| ParamSelFixLambda is the sub-class of ParamSelection that sets the regularization parameter to a constant. More... | |
| class | ParamSelFixSigLam |
| ParamSelFixSigLam is the sub-class of ParamSelection that sets the regularization parameters to constants. More... | |
| class | ParamSelHoDual |
| ParamSelHoDual is the subclass of ParamSelection that implements hold-out cross validation with the dual formulation of RLS. More... | |
| class | ParamSelHoDualr |
| ParamSelHoDualr is the randomized version of ParamSelHoDual. More... | |
| class | ParamSelHoGPRegr |
| ParamSelHoGPRegr is the sub-class of ParamSelection that implements. More... | |
| class | ParamSelHoPrimal |
| ParamSelHoPrimal is the subclass of ParamSelection that implements hold-out cross validation with the primal formulation of RLS. More... | |
| class | ParamSelHoPrimalr |
| ParamSelHoPrimalr is the randomized version of ParamSelHoPrimal. More... | |
| class | ParamSelLoocvDual |
| ParamSelLoocvDual is the sub-class of ParamSelection that implements LOO cross-validation with the dual formulation. More... | |
| class | ParamSelLoocvPrimal |
| ParamSelLoocvPrimal is the sub-class of ParamSelection that implements LOO cross-validation with the primal formulation. More... | |
| class | ParamSelLooGPRegr |
| ParamSelLooGPRegr is the sub-class of ParamSelection that implements. More... | |
| class | ParamSelSiglam |
| ParamSelSiglam is the sub-class of ParamSelection that implements LOO cross-validation with the dual formulation for a rbf kernel. More... | |
| class | ParamSelSiglamHo |
| ParamSelSiglam is the sub-class of ParamSelection that implements hold-out cross validation with the dual formulation for a rbf kernel. More... | |
| class | ParamSelSiglamHoGPRegr |
| ParamSelSiglamHoGPRegr is the sub-class of ParamSelection that implements. More... | |
| class | ParamSelSiglamLooGPRegr |
| ParamSelSiglamLooGPRegr is the sub-class of ParamSelection that implements leave-one-ot parameter selection for Gaussian process regression. More... | |
| class | PerfMacroAvg |
| PerfMacroAvg is the sub-class of Performance that evaluates prediction accuracy. More... | |
| class | Performance |
| Performance is the class that evaluates prediction performance. More... | |
| class | PerfPrecRec |
| PerfPrecRec is the sub-class of Performance that evaluates prediction precision. More... | |
| class | PerfRmse |
| PerfRmse is the sub-class of Performance that evaluates prediction error. More... | |
| class | PredDual |
| PredDual is the sub-class of Prediction that computes the predictions of a linear classifier in the dual formulation. More... | |
| class | PredGPRegr |
| PredGPRegr is the sub-class of Prediction that computes the predictions of GP. More... | |
| class | Prediction |
| Prediction is the class that computes predictions. More... | |
| class | PredKernel |
| PredKernel is the class that computes the kernel matrix for prediction. More... | |
| class | PredKernelTrainTest |
| PredKernelTrainTest is the sub-class of PredKernel that computes the kernel matrix between training and test sets. More... | |
| class | PredPrimal |
| PredPrimal is the sub-class of Prediction that computes the predictions of a linear classifier in the primal formulation. More... | |
| class | PredRandFeats |
| PredRandFeats is the sub-class of Prediction that computes the predictions of the linear classifier stored in opt.rls.W, and obtained the Random Features approach proposed in: Ali Rahimi, Ben Recht; Random Features for Large-Scale Kernel Machines; in Neural Information Processing Systems (NIPS) 2007. More... | |
| class | RandomFeaturesWrapper |
| RLSWrapper is the sub-class of GurlsWrapper that implements Regularized Least Squares with a linear model. More... | |
| class | RecursiveRLSWrapper |
| RecursiveRLSWrapper is the sub-class of GurlsWrapper that implements recursive update of the RLS estimator with retraining capability. More... | |
| class | RLSAuto |
| RLSAuto is the sub-class of Optimizer that implements automatic selection of primal/dual procedure. More... | |
| class | RLSDual |
| RLSDual is the sub-class of Optimizer that implements RLS with the dual formulation. More... | |
| class | RLSDualr |
| RLSDualr is the sub-class of Optimizer that implements RLS with the dual formulation, using a randomized version of SVD. More... | |
| class | RLSGPRegr |
| RLSGPRegr is the sub-class of Optimizer that implements GP inference. More... | |
| class | RLSPegasos |
| RLSPegasos is the sub-class of Optimizer that implements the Pegaosos algorithm. More... | |
| class | RLSPrimal |
| RLSPrimal is the sub-class of Optimizer that implements RLS with the primal formulation. More... | |
| class | RLSPrimalr |
| RLSPrimalr is the sub-class of Optimizer that implements RLS with the primal formulation, using a randomized version of SVD. More... | |
| class | RLSPrimalRecInit |
| RLSPrimalRecInit is the sub-class of Optimizer that implements RLS with the primal formulation. More... | |
| class | RLSPrimalRecUpdate |
| RLSPrimalRecUpdate is the sub-class of Optimizer that implements RLS with the primal formulation. More... | |
| class | RLSRandFeats |
| RLSRandFeats is the sub-class of Optimizer that computes a classifier for the primal formulation of RLS using the Random Features approach proposed in: Ali Rahimi, Ben Recht; Random Features for Large-Scale Kernel Machines; in Neural Information Processing Systems (NIPS) 2007. More... | |
| class | RLSWrapper |
| RLSWrapper is the sub-class of GurlsWrapper that implements Regularized Least Squares with a linear model. More... | |
| class | Split |
| Split is the class that splits data into pair(s) of training and test samples. More... | |
| class | SplitHo |
| SplitHoMulti is the sub-class of Split that splits data into one or more pairs of training and test samples. More... | |
Enumerations | |
| enum | CBLAS_DIAG { CblasNonUnit = 5, CblasUnit = 6 } |
| Diagonal options (unit, non unit) | |
| enum | CBLAS_ORDER { CblasRowMajor = 9, CblasColMajor = 10 } |
| Matrix Order (row major or column major) | |
| enum | CBLAS_SIDE { CblasLeft = 7, CblasRight = 8 } |
| Side options (left, right) | |
| enum | CBLAS_TRANSPOSE { CblasNoTrans = 0, CblasTrans = 1, CblasConjTrans = 2 } |
| Transposition options (no transpose, transpose, conjugate transpose) | |
| enum | CBLAS_UPLO { CblasUpper = 3, CblasLower = 4 } |
| Upper/lower options (upper, lower) | |
| enum | InversionAlgorithm { LU, GaussJ } |
| Implemented inversion algorithms. | |
| enum | OptTypes { GenericOption, StringOption, NumberOption, StringListOption, NumberListOption, FunctionOption, MatrixOption, VectorOption, OptListOption, TaskSequenceOption, TaskIDOption, OptArrayOption, ProcessOption } |
| Enumeration containing all implemented Option types. | |
Functions | |
| template<typename T > | |
| void | argmin (const T *A, unsigned long *result, const int A_rows, const int A_cols, const int res_length) throw (gException) |
| Coputes the smallest elements along the rows of a matrix. | |
| template<typename T > | |
| void | axpy (const int N, const T alpha, const T *X, const int incX, T *Y, const int incY) |
| Template function to call BLAS *AXPY routines. | |
| template<> | |
| GURLS_EXPORT void | axpy (const int N, const float alpha, const float *X, const int incX, float *Y, const int incY) |
| Specialized version of axpy for float buffers. | |
| template<> | |
| GURLS_EXPORT void | axpy (const int N, const double alpha, const double *X, const int incX, double *Y, const int incY) |
| Specialized version of axpy for double buffers. | |
| template<typename T > | |
| void | binOperation (const T *A, const T *B, T *result, const int len, T(*op)(T, T)) |
Applies an element by element binary operation 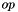 over two vectors ( over two vectors ( 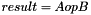 ) ) | |
| template<typename T > | |
| void | cholesky (const gMat2D< T > &A, gMat2D< T > &L, bool upper=true) |
| Computes the Cholesky factorization of a symmetric, positive definite matrix using the LAPACK routine SPOTRF. | |
| template<> | |
| GURLS_EXPORT void | cholesky (const gMat2D< float > &A, gMat2D< float > &L, bool upper) |
| Specialized version of cholesky for float matrices. | |
| template<typename T > | |
| void | cholesky (const T *matrix, const int rows, const int cols, T *result, bool upper=true) |
| Computes the Cholesky factorization of a symmetric, positive definite matrix using the LAPACK routine SPOTRF. | |
| template<typename T > | |
| void | clearLowerTriangular (T *matrix, int rows, int cols) |
| Zeroes on the lower triangle of a matrix. | |
| template<typename T > | |
| T * | compare (const T *vector1, const T *vector2, const int size, bool(*pred)(T, T)) |
| Compares element by element two vectors using a binary predicate, and returns a vector where each element is: | |
| template<typename T > | |
| T * | compare (const T *vector, const T thr, const int size, bool(*pred)(T, T)) |
| Compares each element of a vector with a threshold using a binary predicate and returns a vector where each element is: | |
| template<typename T > | |
| void | copy (T *dst, const T *src, const int size) |
| Copies element form one vector to another one. | |
| template<> | |
| GURLS_EXPORT void | copy (float *dst, const float *src, const int size) |
| Specialized version of copy for float buffers. | |
| template<> | |
| GURLS_EXPORT void | copy (double *dst, const double *src, const int size) |
| Specialized version of copy for double buffers. | |
| template<typename T > | |
| void | copy (T *dst, const T *src, const int size, const int dstIncr, const int srcIncr) |
| Copies element form one vector to another one. | |
| template<> | |
| GURLS_EXPORT void | copy (float *dst, const float *src, const int size, const int dstIncr, const int srcIncr) |
| Specialized version of copy for float buffers. | |
| template<> | |
| GURLS_EXPORT void | copy (double *dst, const double *src, const int size, const int dstIncr, const int srcIncr) |
| Specialized version of copy for double buffers. | |
| template<typename T > | |
| void | copy_submatrix (T *dst, const T *src, const int src_Rows, const int sizeRows, const int sizeCols, unsigned long *indices_rows, unsigned long *indices_cols) |
| Generates a submatrix from an input matrix. | |
| template<typename T > | |
| void | copyLocations (const unsigned long *locs, const T *src, const int locs_len, const int src_len, T *result) |
| Returns a subvector of an input vector, containing elements of the input vector whose index is contained into an indices vector. | |
| template<class MatrixType > | |
| GurlsOption * | copyOptMatrix (const GurlsOption *toCopy) |
| template<typename T > | |
| void | diag (T *vector, const int len, T *result) |
| Returns a squared matrix initialized in the diagonal with values from a vector. | |
| template<typename T > | |
| void | distance (const T *A, const T *B, const int rows, const int A_cols, const int B_cols, T *D) |
| Utility function used to build the kernel matrix; it computes the matrix of the squared euclidean distance between each column of A and each colum of B. | |
| template<typename T > | |
| void | distance_transposed (const T *A, const T *B, const int cols, const int A_rows, const int B_rows, T *D) |
| Utility function used to build the kernel matrix; it computes the matrix of the squared euclidean distance between each row of A and each row of B. | |
| template<typename T > | |
| void | distance_transposed_vm (const T *A, const T *B, const int cols, const int B_rows, T *D, const int size, const int incrA=1) |
| Utility function used to build the kernel matrix; it computes the matrix of the squared euclidean distance between a vector A and each row of B. | |
| template<typename T > | |
| T | div (T a, T b) |
| Division of two scalars. | |
| template<> | |
| GURLS_EXPORT float | dot (const gVec< float > &x, const gVec< float > &y) |
| Specialized version of dot for float vectors. | |
| template<> | |
| GURLS_EXPORT double | dot (const gVec< double > &x, const gVec< double > &y) |
| Specialized version of dot for float vectors. | |
| template<typename T > | |
| void | dot (const gMat2D< T > &A, const gMat2D< T > &B, gMat2D< T > &C) |
| Implements the standard GEMM routine from Level3 BLAS General Matrix-Matrix multiplication of two single/double precision real matrices A and B (the corresponding Matlab code is: C = A*B;). | |
| template<> | |
| GURLS_EXPORT void | dot (const gMat2D< float > &A, const gMat2D< float > &B, gMat2D< float > &C) |
| Specialized version of dot for float matrices. | |
| template<typename T > | |
| T | dot (const int N, const T *X, const int incX, const T *Y, const int incY) |
| Template function to call BLAS *DOT routines. | |
| template<typename T > | |
| void | dot (const gMat2D< T > &A, const gVec< T > &x, gVec< T > &y) |
| Implements the standard DOT routine from Level 1 BLAS General Matrix-Vector multiplication of a single/double precision matrix A with a vector x (the corresponding Matlab code is y = A*x;). | |
| template<> | |
| GURLS_EXPORT void | dot (const gMat2D< double > &A, const gMat2D< double > &B, gMat2D< double > &C) |
| Specialized version of dot for float matrices. | |
| template<typename T > | |
| T | dot (const gVec< T > &x, const gVec< T > &y) |
| Implements the standard scalar product between vectors General routine from Level1 BLAS: n <-- x^T * y General Vector-Vector multiplication for single/double precision real data. | |
| template<> | |
| GURLS_EXPORT void | dot (const gMat2D< float > &A, const gVec< float > &x, gVec< float > &y) |
| Specialized version of dot for float matrices/vectors. | |
| template<> | |
| GURLS_EXPORT float | dot (const int N, const float *X, const int incX, const float *Y, const int incY) |
| Specialized version of dot for float buffers. | |
| template<> | |
| GURLS_EXPORT double | dot (const int N, const double *X, const int incX, const double *Y, const int incY) |
| Specialized version of dot for double buffers. | |
| template<> | |
| GURLS_EXPORT void | dot (const gMat2D< double > &A, const gVec< double > &x, gVec< double > &y) |
| Specialized version of dot for float matrices/vectors. | |
| template<typename T > | |
| void | dot (const T *A, const T *B, T *C, int A_rows, int A_cols, int B_rows, int B_cols, int C_rows, int C_cols, const CBLAS_TRANSPOSE TransA, const CBLAS_TRANSPOSE TransB, const CBLAS_ORDER Order) |
| General Matrix-Matrix multiplication of two single/double precision real matrices A and B. | |
| template<typename T > | |
| void | eig (const gMat2D< T > &A, gMat2D< T > &V, gVec< T > &Wr, gVec< T > &Wi) |
| Implements the computation of the eigenvalues of A using the LAPACK routine SGEEV with default computation of the right eigenvectors. | |
| template<typename T > | |
| void | eig (const gMat2D< T > &A, gMat2D< T > &V, gVec< T > &W) |
| Implements the computation of the eigenvalues of A using the LAPACK routine SGEEV with default computation of the right eigenvectors. | |
| template<typename T > | |
| void | eig (const gMat2D< T > &A, gVec< T > &Wr, gVec< T > &Wi) |
| Implements the computation of the eigenvalues of A. | |
| template<typename T > | |
| void | eig (const gMat2D< T > &A, gVec< T > &W) |
| Implements the computation of the eigenvalues of A. | |
| template<> | |
| GURLS_EXPORT void | eig (const gMat2D< float > &A, gMat2D< float > &V, gVec< float > &Wr, gVec< float > &Wi) |
| Specialized version of eig for float matrices/vectors. | |
| template<> | |
| GURLS_EXPORT void | eig (const gMat2D< float > &A, gMat2D< float > &V, gVec< float > &W) |
| Specialized version of eig for float matrices/vectors. | |
| template<> | |
| GURLS_EXPORT void | eig (const gMat2D< float > &A, gVec< float > &Wr, gVec< float > &Wi) |
| Specialized version of eig for float matrices/vectors. | |
| template<> | |
| GURLS_EXPORT void | eig (const gMat2D< float > &A, gVec< float > &W) |
| Specialized version of eig for float matrices/vectors. | |
| template<typename T > | |
| void | eig_sm (T *A, T *L, int A_rows_cols) throw (gException) |
| Computes the eigenvalues/eigenvectors of a squared and symmetric input matrix. | |
| template<typename T > | |
| bool | eq (T val1, T val2) |
| "Equals" operator between two scalars | |
| template<> | |
| GURLS_EXPORT bool | eq (float val1, float val2) |
| "Equals" operator between two scalars, specialized for float values | |
| template<> | |
| GURLS_EXPORT bool | eq (double val1, double val2) |
| "Equals" operator between two scalars, specialized for double values | |
| template<typename T > | |
| T | eucl_dist (const T *A, const T *B, const int len, T *work) |
| Computes Euclidean distance between two vectors. | |
| static std::string | Exception_Functionality_Not_Implemented (Exception_Incipit+"An attempt to use a functionality that is not implemented yet occurred.") |
| Message displayed when trying to use a non implemented funcionality. | |
| static std::string | Exception_Gurls_Inconsistent_Processes_Number (Exception_Incipit+"The number of elements in the list of processes/tasks is not consistent.") |
| Message displayed when the number of gurls processes and gurls tasks are different. | |
| static std::string | Exception_Gurls_Invalid_ProcessID (Exception_Incipit+"Invalid process ID.") |
| Message displayed when the ID of a process is not found into the gurls process list. | |
| static std::string | Exception_Illegal_Argument_Value (Exception_Incipit+"The value of the input variable is not allowed.") |
| Message displayed when an input parameter has an invalid value. | |
| static std::string | Exception_Illegal_Dynamic_Cast (Exception_Incipit+"An illegal dynamic cast occured.") |
| Message displayed when failing a cast. | |
| static std::string | Exception_Incipit ("ERROR! ") |
| String prefix for all exception messages. | |
| static std::string | Exception_Inconsistent_Size (Exception_Incipit+"An attempt to combine arrays with inconsistent dimensions occurred.") |
| Message displayed when two arrays have inconsistent dimensions. | |
| static std::string | Exception_Index_Out_of_Bound (Exception_Incipit+"Index exceeds matrix dimensions.") |
| Message displayed when trying to access an a vector or matrix with a too large index. | |
| static std::string | Exception_Invalid_Reshape_Arguments (Exception_Incipit+"To RESHAPE the number of elements must not change.") |
| Message displayed when trying to reshape a matrix changing the number of elements. | |
| static std::string | Exception_Invalid_TaskSequence (Exception_Incipit+"Invalid task name specification.") |
| Message displayed when trying to execute an unknown task. | |
| static std::string | Exception_Logical_Operator (Exception_Incipit+"An unknown logical comparison has been required.") |
| Message displayed when trying to use an undefined logical operator for comparison. | |
| static std::string | Exception_Parameter_Already_Definied (Exception_Incipit+"The parameter has been already defined.") |
| Message displayed when an options' parameter has been already defined. | |
| static std::string | Exception_Parameter_Not_Definied_Yet (Exception_Incipit+"The requested parameter has not been defined yet.") |
| Message displayed when an options' parameter has not been defined yet. | |
| static std::string | Exception_Required_Parameter_Missing (Exception_Incipit+"One of the parameters required to run the algorithm is missing.") |
| Message displayed when a required parameter for an algorithm is missing. | |
| static std::string | Exception_Square_Matrix_Required (Exception_Incipit+"An attempt to use a general matrix instead of the required square matrix occurred.") |
| Message displayed when trying to use a non squared matrix where a squared one is required. | |
| static std::string | Exception_Unknown_Function (Exception_Incipit+"Unknown function.") |
| Message displayed when trying to execute an unknown function. | |
| static std::string | Exception_Unknown_Option (Exception_Incipit+"An unknown option has been used.") |
| Message displayed when trying to access a non-existent option. | |
| static std::string | Exception_Unsupported_MatrixType (Exception_Incipit+"Matrix type actually unsupported.") |
| Message displayed when trying to build a matrix with an unsupported element type. | |
| static std::string | Exception_Wrong_Memory_Access (Exception_Incipit+"An attempt to acces a non-existent memory location occurred.") |
| Message displayed when a method tryes to modify an array that is not the owner of its data. | |
| template<typename T > | |
| void | exp (T *v, const int length) |
| In place computation of the exponential for each element of a vector. | |
| template<typename T > | |
| int | gelss (int *m, int *n, int *nrhs, T *a, int *lda, T *b, int *ldb, T *s, T *rcond, int *rank, T *work, int *lwork, int *info) |
| Template function to call LAPACK *GELSS routines. | |
| template<> | |
| GURLS_EXPORT int | gelss (int *m, int *n, int *nrhs, float *a, int *lda, float *b, int *ldb, float *s, float *rcond, int *rank, float *work, int *lwork, int *info) |
| Specialized version of gelss for float buffers. | |
| template<> | |
| GURLS_EXPORT int | gelss (int *m, int *n, int *nrhs, double *a, int *lda, double *b, int *ldb, double *s, double *rcond, int *rank, double *work, int *lwork, int *info) |
| Specialized version of gelss for double buffers. | |
| template<> | |
| GURLS_EXPORT void | gemm (const CBLAS_TRANSPOSE TransA, const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K, const float alpha, const float *A, const int lda, const float *B, const int ldb, const float beta, float *C, const int ldc) |
| Specialized version of gemm for float buffers. | |
| template<> | |
| GURLS_EXPORT void | gemm (const CBLAS_TRANSPOSE TransA, const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K, const double alpha, const double *A, const int lda, const double *B, const int ldb, const double beta, double *C, const int ldc) |
| Specialized version of gemm for double buffers. | |
| template<typename T > | |
| void | gemm (const CBLAS_TRANSPOSE TransA, const CBLAS_TRANSPOSE TransB, const int M, const int N, const int K, const T alpha, const T *A, const int lda, const T *B, const int ldb, const T beta, T *C, const int ldc) |
| Template function to call BLAS *GEMM routines. | |
| template<typename T > | |
| void | gemv (const CBLAS_TRANSPOSE TransA, const int M, const int N, const T alpha, const T *A, const int lda, const T *X, const int incX, const T beta, T *Y, const int incY) |
| Template function to call BLAS *GEMV routines. | |
| template<> | |
| GURLS_EXPORT void | gemv (const CBLAS_TRANSPOSE TransA, const int M, const int N, const float alpha, const float *A, const int lda, const float *X, const int incX, const float beta, float *Y, const int incY) |
| Specialized version of gemv for float buffers. | |
| template<> | |
| GURLS_EXPORT void | gemv (const CBLAS_TRANSPOSE TransA, const int M, const int N, const double alpha, const double *A, const int lda, const double *X, const int incX, const double beta, double *Y, const int incY) |
| Specialized version of gemv for double buffers. | |
| template<typename T > | |
| void | geqp3 (int *m, int *n, T *A, int *lda, int *jpvt, T *tau, T *work, int *lwork, int *info) |
| Template function to call LAPACK *GEQP3 routines. | |
| template<> | |
| GURLS_EXPORT void | geqp3 (int *m, int *n, float *A, int *lda, int *jpvt, float *tau, float *work, int *lwork, int *info) |
| Specialized version of geqp3 for float buffers. | |
| template<> | |
| GURLS_EXPORT void | geqp3 (int *m, int *n, double *A, int *lda, int *jpvt, double *tau, double *work, int *lwork, int *info) |
| Specialized version of geqp3 for double buffers. | |
| template<typename T > | |
| int | gesvd_ (char *jobu, char *jobvt, int *m, int *n, T *a, int *lda, T *s, T *u, int *ldu, T *vt, int *ldvt, T *work, int *lwork, int *info) |
| Template function to call BLAS *GESVD routines. | |
| template<> | |
| GURLS_EXPORT int | gesvd_ (char *jobu, char *jobvt, int *m, int *n, float *a, int *lda, float *s, float *u, int *ldu, float *vt, int *ldvt, float *work, int *lwork, int *info) |
| Specialized version of gesvd_ for float buffers. | |
| template<> | |
| GURLS_EXPORT int | gesvd_ (char *jobu, char *jobvt, int *m, int *n, double *a, int *lda, double *s, double *u, int *ldu, double *vt, int *ldvt, double *work, int *lwork, int *info) |
| Specialized version of gesvd_ for double buffers. | |
| template<class Matrix > | |
| OptMatrixBase::MatrixType | getMatrixCellType () |
| template<> | |
| GURLS_EXPORT OptMatrixBase::MatrixType | getMatrixCellType< const gMat2D< double > > () |
| template<> | |
| GURLS_EXPORT OptMatrixBase::MatrixType | getMatrixCellType< const gMat2D< float > > () |
| template<> | |
| GURLS_EXPORT OptMatrixBase::MatrixType | getMatrixCellType< gMat2D< double > > () |
| template<> | |
| GURLS_EXPORT OptMatrixBase::MatrixType | getMatrixCellType< gMat2D< float > > () |
| template<> | |
| GURLS_EXPORT OptMatrixBase::MatrixType | getMatrixCellType< gMat2D< unsigned long > > () |
| template<typename T > | |
| void | getRow (const T *M, const int rows, const int cols, const int row_index, T *row) |
| Generates a vector containing a copy of a row of an input matrix. | |
| template<typename T > | |
| void | GInverseDiagonal (const T *Q, const T *L, const T *lambda, T *Z, const int Q_rows, const int Q_cols, const int L_length, const int lambda_length) |
| template<typename T > | |
| void | GInverseDiagonal (const T *Q, const T *L, const T *lambda, T *Z, const int Q_rows, const int Q_cols, const int L_length, const int lambda_length, T *work) |
| template<typename T > | |
| bool | gt (T a, T b) |
| "Greater than" operator between two scalars | |
| template<> | |
| GURLS_EXPORT bool | gt (float a, float b) |
| "Greater than" operator between two scalars, specialized for float values | |
| template<> | |
| GURLS_EXPORT bool | gt (double a, double b) |
| "Greater than" operator between two scalars, specialized for double values | |
| template<typename T > | |
| bool | gte (T a, T b) |
| "Greater than or equals" operator between two scalars | |
| template<typename T > | |
| void | indicesOfEqualsTo (const T *V, const int len, const T value, unsigned long *ind, int &ind_length) |
| Computes a vector containing the indices of all elements of an input vector that are equals to a given value. | |
| template<typename T > | |
| void | indicesOfMax (const T *A, const int A_rows, const int A_cols, unsigned long *ind, T *work, const int dimension) throw (gException) |
| Returns the indices of the largest elements along different dimensions of a matrix. | |
| template<> | |
| GURLS_EXPORT void | inv (const gMat2D< float > &A, gMat2D< float > &Ainv, InversionAlgorithm alg) |
| Specialized version of inv for float matrices. | |
| template<typename T > | |
| void | inv (const gMat2D< T > &A, gMat2D< T > &Ainv, InversionAlgorithm alg=LU) |
Computes the inverse 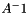 of a matrix of a matrix 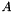 . . | |
| template<typename T > | |
| T * | lambdaguesses (const T *eigvals, const int len, const int r, const int n, const int nlambda, const T minl) |
| Builds array of possible values for the regularization parameter, generating a geometric series from the values in EIGVALS Internal function, not to be called from gurls. | |
| template<typename T > | |
| bool | le (T a, T b) |
| "Less or equal than" operator between two scalars | |
| template<typename T > | |
| void | linspace (T a, T b, unsigned long n, T *res) |
| Generates a row vector of n points linearly spaced between and including a and b. | |
| template<typename T > | |
| bool | lt (T a, T b) |
| "Less than" operator between two scalars | |
| template<> | |
| GURLS_EXPORT bool | lt (float a, float b) |
| "Less than" operator between two scalars, specialized for float values | |
| template<> | |
| GURLS_EXPORT bool | lt (double a, double b) |
| "Less than" operator between two scalars, specialized for double values | |
| template<typename T > | |
| void | lu (gMat2D< T > &A) |
| Implements the LU decomposition usig LAPACK routines. | |
| template<typename T > | |
| void | lu (gMat2D< T > &A, gVec< int > &pv) |
| Implements the LU factorization of a general M-by-N matrix A using partial pivoting with row interchanges, using LAPACK routines. | |
| template<> | |
| GURLS_EXPORT void | lu (gMat2D< float > &A, gVec< int > &pv) |
| Specialized version of lu for float matrices/vectors. | |
| template<> | |
| GURLS_EXPORT void | lu (gMat2D< float > &A) |
| Specialized version of lu for float matrices. | |
| template<typename T > | |
| void | maxValues (const T *A, const int A_rows, const int A_cols, T *maxv, T *work, const int dimension) throw (gException) |
| Returns the largest elements along different dimensions of a matrix. | |
| template<typename T > | |
| void | mean (const T *A, T *result, const int A_rows, const int A_cols, const int res_length) throw (gException) |
| Computes the mean values along the rows of a matrix. | |
| template<typename T > | |
| T | median (T *v, const int length) |
| Returns the median value of a vector. | |
| template<typename T > | |
| void | median (const T *M, const int rows, const int cols, const int dimension, T *res, T *work) |
| Computes the median values of the elements along different dimensions of a matrix. | |
| template<typename T > | |
| void | mldivide_squared (const T *A, T *B, const int a_rows, const int a_cols, const int b_rows, const int b_cols, const CBLAS_TRANSPOSE transA) |
| Performs left division of squared matrices. | |
| template<typename T > | |
| T | mul (T a, T b) |
| Multiplication of two scalars. | |
| template<typename T > | |
| void | mult (const T *A, const T *B, T *result, const int len) |
| Element by element multiplication of two vectors. | |
| template<typename T > | |
| T | norm (const gVec< T > &x, std::string type="l2") |
| Computes a vector norm specified by type parameter. | |
| template<typename T > | |
| T | norm (const gMat2D< T > &A, std::string type="l2") |
| Computes a matrix norm specified by type parameter. | |
| template<typename T > | |
| T | nrm2 (const int N, const T *X, const int incX) |
| Template function to call BLAS *NRM2 routines. | |
| template<> | |
| GURLS_EXPORT float | nrm2 (const int N, const float *X, const int incX) |
| Specialized version of nrm2 for float buffers. | |
| template<> | |
| GURLS_EXPORT double | nrm2 (const int N, const double *X, const int incX) |
| Specialized version of nrm2 for double buffers. | |
| template<typename T > | |
| gVec< T > | operator* (T val, const gVec< T > &v) |
| Returns a vector containing the multiplication of a vector by a scalar. | |
| template<typename T > | |
| gMat2D< T > | operator* (T val, const gMat2D< T > &v) |
| Returns a matrix containing the multiplication of a matrix by a scalar. | |
| template<typename T > | |
| gVec< T > | operator+ (T val, const gVec< T > &v) |
| Returns a vector containing the sum between a vector and a scalar. | |
| template<typename T > | |
| gMat2D< T > | operator+ (T val, const gMat2D< T > &v) |
| Returns a matrix containing the sum between a matrix and a scalar. | |
| template<typename T > | |
| gVec< T > | operator- (T val, const gVec< T > &v) |
| Returns a vector containing the difference between a vector and a scalar. | |
| template<typename T > | |
| gMat2D< T > | operator- (T val, const gMat2D< T > &v) |
| Returns a matrix containing the difference between a matrix and a scalar. | |
| template<typename T > | |
| gMat2D< T > | operator/ (T val, const gMat2D< T > &v) |
| Returns a matrix containing the division of a matrix by a scalar. | |
| template<typename T > | |
| gVec< T > | operator/ (T val, const gVec< T > &v) |
| Returns a vector containing the division of a vector by a scalar. | |
| GURLS_EXPORT std::ostream & | operator<< (std::ostream &os, const GurlsOption &opt) |
| Writes a GurlsOption to a stream. | |
| GURLS_EXPORT std::ostream & | operator<< (std::ostream &os, const OptArray &opt) |
| Writes an OptArray to a stream. | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &os, const gVec< T > &v) |
| Writes vector's information and data to a stream. | |
| GURLS_EXPORT std::ostream & | operator<< (std::ostream &os, const GurlsOptionsList &opt) |
| Writes a GurlsOptionsList to a stream. | |
| template<typename T > | |
| std::ostream & | operator<< (std::ostream &os, const gMat2D< T > &v) |
| Writes matrix information and data to a stream. | |
| template<typename U > | |
| bool | operator== (const BaseArray< U > &v, const U &val) |
| Checks if all elements in a vector are equal to a given value. | |
| template<typename U > | |
| bool | operator== (const gVec< U > &v, const U &val) |
| Checks if all elements in a vector are equal to a given value. | |
| template<typename T > | |
| void | orgqr (int *m, int *n, int *k, T *a, int *lda, T *tau, T *work, int *lwork, int *info) |
| Template function to call LAPACK *ORGQR routines. | |
| template<> | |
| GURLS_EXPORT void | orgqr (int *m, int *n, int *k, float *a, int *lda, float *tau, float *work, int *lwork, int *info) |
| Specialized version of orogqr for float buffers. | |
| template<> | |
| GURLS_EXPORT void | orgqr (int *m, int *n, int *k, double *a, int *lda, double *tau, double *work, int *lwork, int *info) |
| Specialized version of orgqr for double buffers. | |
| template<typename T > | |
| void | pdist (const T *A, const int N, const int P, T *D) |
| Computes a vector D containing the Euclidean distances between each pair of observations in the N-by-P data matrix A. | |
| template<typename T > | |
| void | pinv (const gMat2D< T > &A, gMat2D< T > &Ainv, T RCOND=0) |
| Computes the pseudo-inverse of a non square matrix A. | |
| template<> | |
| GURLS_EXPORT void | pinv (const gMat2D< float > &A, gMat2D< float > &Ainv, float RCOND) |
| Specialized version of pinv for float matrices. | |
| template<typename T > | |
| T * | pinv (const T *A, const int rows, const int cols, int &res_rows, int &res_cols, T *RCOND=NULL) |
| Computes the pseudo-inverse of a matrix. | |
| template<typename T > | |
| int | potrf_ (char *UPLO, int *n, T *a, int *lda, int *info) |
| Template function to call LAPACK *POTRF routines. | |
| template<> | |
| GURLS_EXPORT int | potrf_ (char *UPLO, int *n, float *a, int *lda, int *info) |
| Specialized version of potrf_ for float buffers. | |
| template<> | |
| GURLS_EXPORT int | potrf_ (char *UPLO, int *n, double *a, int *lda, int *info) |
| Specialized version of potrf_ for double buffers. | |
| template<typename T > | |
| T | precrec_driver (const T *out, const T *gt, const unsigned long N, T *work) |
| Utility function called by the class PrecisionRecall to evaluate the average precision through precision and recall. | |
| template<typename T > | |
| T | precrec_driver (const T *out, const T *gt, const unsigned long N) |
| Utility function called by the class PrecisionRecall to evaluate the average precision through precision and recall. | |
| template<typename T > | |
| void | qr_econ (const T *A, int m, int n, T *Q, T *R, int *E) |
| Computes an economy-size QR decomposition of an input matrix A so that A(:,E) = Q*R. | |
| template<typename T > | |
| void | random_svd (const T *A, const unsigned long A_rows, const unsigned long A_cols, T *U, T *S, T *V, unsigned long k=6, unsigned long its=2, unsigned long l=0) |
| Constructs a nearly optimal rank-k approximation USV' to A, using its full iterations of a block Lanczos method of block size l, started with an n x l random matrix, when A is m x n;. | |
| template<typename T > | |
| void | randperm (const unsigned long n, T *seq, bool generate=true, unsigned long start=1) |
| Generates a vector containing a random permutation of the values from start to start+n inclusive. | |
| template<typename T > | |
| void | rdivide (const T *A, const T *B, T *result, const int len) |
| Element by element division of two vectors. | |
| template<typename T > | |
| gMat2D< T > | repmat (const gVec< T > &x, unsigned long n, bool transpose=false) |
| Replicates a vector n times along the columns (or along the rows if transpose==true) If x is a vector of length N, then the output is an N-by-N matrix whose columns (or rows) are copies of x. | |
| template<typename T > | |
| void | rls_eigen (const T *Q, const T *L, const T *Qty, T *C, const T lambda, const int n, const int Q_rows, const int Q_cols, const int L_length, const int Qty_rows, const int Qty_cols) |
| Computes RLS estimator given the singular value decomposition of the kernel matrix. | |
| template<typename T > | |
| void | rls_eigen (const T *Q, const T *L, const T *Qty, T *C, const T lambda, const int n, const int Q_rows, const int Q_cols, const int L_length, const int Qty_rows, const int Qty_cols, T *work) |
| Computes RLS estimator given the singular value decomposition of the kernel matrix. | |
| template<typename T > | |
| GurlsOptionsList * | rls_pegasos_driver (const T *X, const T *bY, const GurlsOptionsList &opt, const int X_rows, const int X_cols, const int bY_rows, const int bY_cols) |
| Utility function called by the class RLSPegasos to implement a single pass for pegasos algorithm, performing the stochastic gradient descent over all training samples once. | |
| template<typename T > | |
| gMat2D< T > * | rls_primal_driver (T *K, const T *Xty, const unsigned long n, const unsigned long d, const unsigned long Yd, const T lambda) |
| template<typename T > | |
| int | round (const T value) |
| Rounds an input value to the nearest integer. | |
| template<typename T > | |
| gMat2D< T > * | rp_apply_real (const T *X, const T *W, const unsigned long n, const unsigned long d, const unsigned long D) |
| template<typename T > | |
| gMat2D< T > * | rp_apply_real (const gMat2D< T > &X, const gMat2D< T > &W) |
| template<typename T > | |
| gMat2D< T > * | rp_factorize_large_real (const gMat2D< T > &X, const gMat2D< T > &y, const unsigned long D, const unsigned long psize, T *XtX, T *Xty) |
| template<typename T > | |
| gMat2D< T > * | rp_projections (const unsigned long d, const unsigned long D) |
| template<typename T > | |
| void | scal (const int N, const T alpha, T *X, const int incX) |
| Template function to call BLAS *SCAL routines. | |
| template<> | |
| GURLS_EXPORT void | scal (const int N, const float alpha, float *X, const int incX) |
| Specialized version of scal for float buffers. | |
| template<> | |
| GURLS_EXPORT void | scal (const int N, const double alpha, double *X, const int incX) |
| Specialized version of scal for double buffers. | |
| template<typename T > | |
| void | set (T *buffer, const T value, const int size, const int incr) |
| Sets elements of a vector to a specified value. | |
| template<typename T > | |
| void | set (T *buffer, const T value, const int size) |
| Sets all elements of a vector to a specified value. | |
| template<> | |
| void GURLS_EXPORT | set (float *buffer, const float value, const int size) |
| Specialized version of set for float buffers. | |
| template<> | |
| void GURLS_EXPORT | set (double *buffer, const double value, const int size) |
| Specialized version of set for double buffers. | |
| template<> | |
| void GURLS_EXPORT | set (float *buffer, const float value, const int size, const int incr) |
| Specialized version of set for float buffers. | |
| template<> | |
| void GURLS_EXPORT | set (double *buffer, const double value, const int size, const int incr) |
| Specialized version of set for double buffers. | |
| template<typename T > | |
| void | setReciprocal (T *matrix, const int len) |
| Computes the element-by-element multiplicative inverse of an input matrix. | |
| template<typename T > | |
| T * | sign (const T *vector, const int size) |
| Computes a "signum vector" of the same size as an input vector, where each element is: | |
| template<typename T > | |
| void | sort (const T *M, const unsigned long rows, const unsigned long cols, bool(*pred)(T, T), T *values, unsigned long *indices) |
| Sorts the elements of a matrix along the columns. | |
| template<typename T > | |
| void | squareform (const T *A, const int N, const int P, T *D, const int d_cols) |
| Reformats a distance matrix between upper triangular and square form. | |
| template<typename T > | |
| void | stdDev (const T *X, const int rows, const int cols, T *res, T *work) |
| Generates a row vector containing the standard deviation of the elements of each column of an input matrix. | |
| template<typename T > | |
| void | subMatrixFromColumns (const T *matrix, const int mRows, const int mCols, const unsigned long *colsIndices, const int nIndices, T *submat) |
| Generates a submatrix from an input matrix. | |
| template<typename T > | |
| void | subMatrixFromRows (const T *matrix, const int mRows, const int mCols, const unsigned long *rowsIndices, const int nIndices, T *submat) |
| Generates a submatrix from an input matrix. | |
| template<typename T > | |
| void | sum (const T *A, T *result, const int A_rows, const int A_cols, const int res_length) throw (gException) |
| Sums all elements along the rows of a matrix. | |
| template<typename T > | |
| void | sum_col (const T *A, T *result, const int A_rows, const int A_cols) throw (gException) |
| Sums all elements along the columns of a matrix. | |
| template<typename T > | |
| T | sumv (const T *V, const int len) throw (gException) |
| Computes the sum of all elements of a vector. | |
| template<typename T > | |
| void | svd (const gMat2D< T > &A, gMat2D< T > &U, gVec< T > &W, gMat2D< T > &Vt) |
| Implements the SVD decomposition of a general rectangular matrix: A = U*W*Vt. | |
| template<> | |
| GURLS_EXPORT void | svd (const gMat2D< float > &A, gMat2D< float > &U, gVec< float > &W, gMat2D< float > &Vt) |
| Specialized version of svd for float matrices/vectors. | |
| template<typename T > | |
| void | svd (const T *A, T *&U, T *&S, T *&Vt, const int A_rows, const int A_cols, int &U_rows, int &U_cols, int &S_len, int &Vt_rows, int &Vt_cols, bool econ=false) throw (gException) |
| Computes singular value decomposition of an input matrix A such that A = U*diag(S)*Vt. | |
| template<typename T > | |
| void | swap (int n, T *x, int incx, T *y, int incy) |
| Template function to call BLAS *SWAP routines. | |
| template<> | |
| GURLS_EXPORT void | swap (int n, float *x, int incx, float *y, int incy) |
| Specialized version of swap for float buffers. | |
| template<> | |
| GURLS_EXPORT void | swap (int n, double *x, int incx, double *y, int incy) |
| Specialized version of swap for double buffers. | |
| template<typename T > | |
| void | syev (char *jobz, char *uplo, int *n, T *a, int *lda, T *w, T *work, int *lwork, int *info) |
| Template function to call LAPACK *SYEV routines. | |
| template<> | |
| GURLS_EXPORT void | syev (char *jobz, char *uplo, int *n, float *a, int *lda, float *w, float *work, int *lwork, int *info) |
| Specialized version of syev for float buffers. | |
| template<> | |
| GURLS_EXPORT void | syev (char *jobz, char *uplo, int *n, double *a, int *lda, double *w, double *work, int *lwork, int *info) |
| Specialized version of syev for double buffers. | |
| static const std::string | TASKDESC_SEPARATOR (":") |
| String used to tokenize task strings (e.g. | |
| template<typename T > | |
| T | test_classifier (T *W, GurlsOptionsList &opt, const int rows, const int cols) |
| Utility function called by the rls_pegasos_driver; it evaluate classification accuracy on the test set given in fields Xte and yte of opt. | |
| template<typename T > | |
| void | transpose (const T *matrix, const int rows, const int cols, T *transposed) |
| Transpose a matrix. | |
| template<typename T > | |
| void | trsm (const CBLAS_SIDE Side, const CBLAS_UPLO Uplo, const CBLAS_TRANSPOSE TransA, const CBLAS_DIAG Diag, const int M, const int N, const T alpha, const T *A, const int lda, T *B, const int ldb) |
| Template function to call BLAS *TRSM routines. | |
| template<> | |
| GURLS_EXPORT void | trsm (const CBLAS_SIDE Side, const CBLAS_UPLO Uplo, const CBLAS_TRANSPOSE TransA, const CBLAS_DIAG Diag, const int M, const int N, const float alpha, const float *A, const int lda, float *B, const int ldb) |
| Specialized version of trsm for float buffers. | |
| template<> | |
| GURLS_EXPORT void | trsm (const CBLAS_SIDE Side, const CBLAS_UPLO Uplo, const CBLAS_TRANSPOSE TransA, const CBLAS_DIAG Diag, const int M, const int N, const double alpha, const double *A, const int lda, double *B, const int ldb) |
| Specialized version of trsm for double buffers. | |
Variables | |
| static const int | COLUMNWISE = 0 |
| Used to tell methods to operate on a matrix in column-wise order. | |
| static const std::string | L0norm = "l0" |
| String identifying l0-norm. | |
| static const std::string | L1norm = "l1" |
| String identifying l1-norm. | |
| static const std::string | L2norm = "l2" |
| String identifying l2-norm. | |
| static const std::string | LInfnorm = "inf" |
| String identifying infinity-norm. | |
| static const int | MAX_PRINTABLE_SIZE = 200 |
| Maximum vector size for printing. | |
| static const int | ROWWISE = 1 |
| Used to tell methods to operate on a matrix in row-wise order. | |
The namespace gurls comprises all the classes, constants, typedefs, and functions currently available within the library.
| void gurls::argmin | ( | const T * | A, |
| unsigned long * | result, | ||
| const int | A_rows, | ||
| const int | A_cols, | ||
| const int | res_length | ||
| ) | throw (gException) |
| A | input matrix |
| result | vecotr of length A_cols containing the smallest elements for each row of the matrix |
| A_rows | number of rows of matrix A |
| A_cols | number of columns of matrix A |
| res_length | results vector length (MUST be == A_cols) |
Definition at line 874 of file gmath.h.
{
if(A_cols != res_length)
throw gException(Exception_Inconsistent_Size);
const T *a_it = A;
for(unsigned long *r_it = result, *r_end = result+A_cols; r_it != r_end; ++r_it, a_it += A_rows)
*r_it = (std::min_element(a_it, a_it+A_rows) - a_it);
}
| void gurls::binOperation | ( | const T * | A, |
| const T * | B, | ||
| T * | result, | ||
| const int | len, | ||
| T(*)(T, T) | op | ||
| ) |
| A | first input vector |
| B | second input vector |
| result | vector |
| len | vectors length |
| op | binary operation to perform |
Definition at line 747 of file gmath.h.
{
const T *a_it = A, *a_end = A+len;
const T *b_it = B;
T *r_it = result;
while(a_it != a_end)
{
*r_it = (*op)((*a_it),(*b_it));
++a_it;
++b_it;
++r_it;
}
}
| void gurls::cholesky | ( | const T * | matrix, |
| const int | rows, | ||
| const int | cols, | ||
| T * | result, | ||
| bool | upper = true |
||
| ) |
| matrix | input matrix |
| rows | number of rows of the input matrix |
| cols | number of columns of the input matrix |
| upper | whether to store the upper or the lower triangle of the result matrix |
| resyult | Cholesky factorization of the input matrix |
Definition at line 586 of file gmath.h.
{
copy(result, matrix, rows*cols);
int LDA = rows;
int nc = cols;
char UPLO = upper? 'U':'L';
int info;
potrf_(&UPLO, &nc, result, &LDA, &info);
if(info != 0)
{
std::stringstream str;
str << "Cholesky factorization failed, error code " << info << ";" << std::endl;
throw gException(str.str());
}
clearLowerTriangular(result, rows, cols);
}
| void gurls::clearLowerTriangular | ( | T * | matrix, |
| int | rows, | ||
| int | cols | ||
| ) |
| T* gurls::compare | ( | const T * | vector1, |
| const T * | vector2, | ||
| const int | size, | ||
| bool(*)(T, T) | pred | ||
| ) |
| vector1 | first input vector |
| vector2 | second input vector |
| size | number of elements of the input vectors |
| pred | binary predicate used for comparison |
Definition at line 1044 of file gmath.h.
{
const T* v1_end = vector1+size;
T* ret = new T[size];
T* r_it = ret;
const T zero = static_cast<T>(0.0);
const T one = static_cast<T>(1.0);
for(const T *v1_it = vector1, *v2_it = vector2; v1_it != v1_end; ++v1_it, ++v2_it, ++r_it)
*r_it = (*pred)(*v1_it, *v2_it)? one: zero;
return ret;
}
| T* gurls::compare | ( | const T * | vector, |
| const T | thr, | ||
| const int | size, | ||
| bool(*)(T, T) | pred | ||
| ) |
| vector | input vector |
| thr | threshold |
| size | number of elements of the input vector |
| pred | binary predicate used for comparison |
Definition at line 1074 of file gmath.h.
{
const T* v1_end = vector+size;
T* ret = new T[size];
T* r_it = ret;
const T zero = static_cast<T>(0.0);
const T one = static_cast<T>(1.0);
for(const T *v1_it = vector; v1_it != v1_end; ++v1_it, ++r_it)
*r_it = (*pred)(*v1_it, thr)? one: zero;
return ret;
}
| void gurls::copy | ( | T * | dst, |
| const T * | src, | ||
| const int | size | ||
| ) |
| void gurls::copy | ( | T * | dst, |
| const T * | src, | ||
| const int | size, | ||
| const int | dstIncr, | ||
| const int | srcIncr | ||
| ) |
| dst | destination vector |
| src | source vector |
| size | number of copies to be performed |
| dstIncr | iteration increment on destination buffer |
| srcIncr | iteration increment on source buffer |
Definition at line 293 of file gmath.h.
{
if(dstIncr == 1 && srcIncr == 1)
copy(dst, src, size);
else
{
const T* s_it = src;
for(T *d_it = dst, *end = dst+(size*dstIncr); d_it != end; d_it += dstIncr, src+=srcIncr)
*d_it = *s_it;
}
}
| void gurls::copy_submatrix | ( | T * | dst, |
| const T * | src, | ||
| const int | src_Rows, | ||
| const int | sizeRows, | ||
| const int | sizeCols, | ||
| unsigned long * | indices_rows, | ||
| unsigned long * | indices_cols | ||
| ) |
| dst | output submatrix |
| src | input matrix |
| src_Rows | number of rows of the input matrix |
| sizeRows | number of rows of the output submatrix |
| sizeCols | number of columns of the output submatrix |
| indices_rows | vector containing the row indices to copy (length must be == sizeRows) |
| indices_cols | vector containing the column indices to copy (length must be == sizeCols) |
Definition at line 331 of file gmath.h.
{
int t=0;
for (int j = 0; j < sizeCols; ++j)
for (int i = 0; i < sizeRows; ++i)
{
dst[t] = src[ indices_rows[i] + indices_cols[j]*src_Rows ];
++t;
}
}
| void gurls::copyLocations | ( | const unsigned long * | locs, |
| const T * | src, | ||
| const int | locs_len, | ||
| const int | src_len, | ||
| T * | result | ||
| ) |
| locs | indices vector |
| src | input vector |
| locs_len | length of the indices vector |
| src_len | length of the input vector |
| result | on exit it contains a subvector with all elements of the input vector whose index is contained into locs |
Definition at line 895 of file gmath.h.
{
T* ptr_v = result;
int val;
for(const unsigned long* l_it = locs, *l_end=locs+locs_len; l_it != l_end; ++l_it, ++ptr_v)
{
val = *l_it;
if((val < 0) || (val > src_len))
throw gException(gurls::Exception_Index_Out_of_Bound);
*ptr_v = src[val];
}
}
| void gurls::diag | ( | T * | vector, |
| const int | len, | ||
| T * | result | ||
| ) |
| void gurls::distance | ( | const T * | A, |
| const T * | B, | ||
| const int | rows, | ||
| const int | A_cols, | ||
| const int | B_cols, | ||
| T * | D | ||
| ) |
| A | matrix |
| B | matrix |
| rows | number of rows of both A and B |
| A_cols | number of columns of A |
| B_cols | number of columns of B |
| D | output A_colsxB_cols kernel matrix |
Definition at line 422 of file utils.h.
{
set(D, (T)0.0, A_cols*B_cols);
//for i = 1:na
for(int i=0; i< A_cols; ++i)
// for j = 1:nb
for(int j=0; j< B_cols; ++j)
// for k = 1:dim_a
for(int k=0; k<rows; ++k)
{
// d(i,j) = d(i,j) + (a(k,i) - b(k,j))^2;
const double diff = A[k+rows*i]-B[k+rows*j];
D[i+A_cols*j] += diff*diff;
}
}
| void gurls::distance_transposed | ( | const T * | A, |
| const T * | B, | ||
| const int | cols, | ||
| const int | A_rows, | ||
| const int | B_rows, | ||
| T * | D | ||
| ) |
| A | matrix |
| B | matrix |
| cols | number of cols of both A and B |
| A_rows | number of rows of A |
| B_rows | number of rows of B |
| D | output A_rowsxB_rows kernel matrix |
Definition at line 451 of file utils.h.
{
set(D, (T)0.0, A_rows*B_rows);
for(int i=0; i< A_rows; ++i)
for(int j=0; j< B_rows; ++j)
for(int k=0; k<cols; ++k)
{
// d(i,j) = d(i,j) + (a(i,k) - b(j,k))^2;
const T diff = A[i+A_rows*k]-B[j+B_rows*k];
D[i+A_rows*j] += diff*diff;
}
}
| void gurls::distance_transposed_vm | ( | const T * | A, |
| const T * | B, | ||
| const int | cols, | ||
| const int | B_rows, | ||
| T * | D, | ||
| const int | size, | ||
| const int | incrA = 1 |
||
| ) |
| A | vector |
| B | matrix |
| cols | number of cols of both A and B |
| B_rows | number of rows of B |
| D | output of length "size" |
| size | length of vector D |
| incrA | specifies the increment for indexing vector A |
Definition at line 478 of file utils.h.
{
int j;
//#pragma omp parallel for private(j)
for(j=0; j< size; ++j)
{
const T* B_it = B+j;
const T* A_it = A;
T Dj = 0;
for(int k=0; k<cols; ++k)
{
// d(j) = d(j) + (a(k) - b(j,k))^2;
const T diff = *A_it - *B_it;
Dj += diff*diff;
A_it += incrA;
B_it += B_rows;
}
D[j] = Dj;
}
}
| void gurls::dot | ( | const gMat2D< T > & | A, |
| const gMat2D< T > & | B, | ||
| gMat2D< T > & | C | ||
| ) |
| [in] | A | Left matrix |
| [in] | B | Right matrix |
| [out] | C | Product Matrix |
| void gurls::dot | ( | const gMat2D< T > & | A, |
| const gVec< T > & | x, | ||
| gVec< T > & | y | ||
| ) |
| [in] | A | Input matrix |
| [in] | x | Input vector |
| [out] | y | Output vector |
| void gurls::dot | ( | const T * | A, |
| const T * | B, | ||
| T * | C, | ||
| int | A_rows, | ||
| int | A_cols, | ||
| int | B_rows, | ||
| int | B_cols, | ||
| int | C_rows, | ||
| int | C_cols, | ||
| const CBLAS_TRANSPOSE | TransA, | ||
| const CBLAS_TRANSPOSE | TransB, | ||
| const CBLAS_ORDER | Order | ||
| ) |
| [in] | A | Left matrix |
| [in] | B | Right matrix |
| [out] | C | Product Matrix |
| [in] | A_rows | numer of rows of the matrix A |
| [in] | A_cols | numer of columns of the matrix A |
| [in] | B_rows | numer of rows of the matrix B |
| [in] | B_cols | numer of columns of the matrix B |
| [in] | C_rows | numer of rows of the matrix C |
| [in] | C_cols | numer of columns of the matrix C |
| [in] | TransA | Transposition option form matrix A |
| [in] | TransB | Transposition option form matrix B |
| [in] | Order | order option for matrix multiplication |
Definition at line 516 of file gmath.h.
{
bool transposeA = (TransA == CblasTrans || TransA == CblasConjTrans);
bool transposeB = (TransB == CblasTrans || TransB == CblasConjTrans);
if(transposeA)
std::swap(A_rows, A_cols);
if(transposeB)
std::swap(B_rows, B_cols);
if ((C_rows != A_rows) || (C_cols != B_cols))
throw gException(gurls::Exception_Inconsistent_Size);
if (A_cols != B_rows)
throw gException(gurls::Exception_Inconsistent_Size);
const T alpha = 1.0;
const T beta = 0.0;
int lda, ldb, ldc;
int k = A_cols;
// mxk kxn mxn
switch(Order)
{
case CblasColMajor:
lda = transposeA? k: A_rows;
ldb = transposeB? B_cols: k;
ldc = C_rows;
gemm(TransA, TransB, A_rows, B_cols, k, alpha, A, lda, B, ldb, beta, C, ldc);
break;
case CblasRowMajor:
lda = transposeA? A_rows: k;
ldb = transposeB? k: B_cols;
ldc = C_cols;
gemm(TransB, TransA, B_cols, A_rows, k, alpha, B, ldb, A, lda, beta, C, ldc);
break;
default:
lda = ldb = ldc = 0;
assert(0);
}
}
| void gurls::eig_sm | ( | T * | A, |
| T * | L, | ||
| int | A_rows_cols | ||
| ) | throw (gException) |
| A | input matrix. On exit it contains the orthonormal eigenvectors of the matrix A |
| L | vector of eigenvalues in ascending order |
| A_rows_cols | number of rows/columns of matrix A |
Definition at line 1444 of file gmath.h.
{
char jobz = 'V';
char uplo = 'L';
int n = A_rows_cols, lda = n;
int info, lwork = 4*n;
T* work = new T[lwork];
syev(&jobz, &uplo, &n, A, &lda, L, work, &lwork, &info );
delete[] work;
if(info != 0)
{
std::stringstream str;
str << "Eigenvalues/eigenVectors computation failed, error code " << info << ";" << std::endl;
throw gException(str.str());
}
}
| GURLS_EXPORT bool gurls::eq | ( | float | val1, |
| float | val2 | ||
| ) |
| GURLS_EXPORT bool gurls::eq | ( | double | val1, |
| double | val2 | ||
| ) |
| T gurls::eucl_dist | ( | const T * | A, |
| const T * | B, | ||
| const int | len, | ||
| T * | work | ||
| ) |
| void gurls::exp | ( | T * | v, |
| const int | length | ||
| ) |
| void gurls::getRow | ( | const T * | M, |
| const int | rows, | ||
| const int | cols, | ||
| const int | row_index, | ||
| T * | row | ||
| ) |
| M | input matrix |
| rows | number of rows of the input matrix |
| cols | number of columns of the input matrix |
| row_index | index of the row to be extracted |
| row | vector containing the extracted row. Length must be equal to cols |
Definition at line 1431 of file gmath.h.
{
copy(row, M+row_index, cols, 1, rows);
}
| GURLS_EXPORT bool gurls::gt | ( | float | a, |
| float | b | ||
| ) |
| GURLS_EXPORT bool gurls::gt | ( | double | a, |
| double | b | ||
| ) |
| void gurls::indicesOfEqualsTo | ( | const T * | V, |
| const int | len, | ||
| const T | value, | ||
| unsigned long * | ind, | ||
| int & | ind_length | ||
| ) |
| V | input vector |
| len | number of elements of the input vector |
| value | value for comparison |
| ind | vector of the indices. Length must be >= len |
| ind_length | total number of indices written into ind |
Definition at line 1585 of file gmath.h.
{
unsigned long* r_it = ind;
for(const T *it = V, *end = V+len; it != end; ++it)
{
if(eq(*it, value))
{
*r_it = it-V;
++r_it;
}
}
ind_length = r_it - ind;
}
| void gurls::indicesOfMax | ( | const T * | A, |
| const int | A_rows, | ||
| const int | A_cols, | ||
| unsigned long * | ind, | ||
| T * | work, | ||
| const int | dimension | ||
| ) | throw (gException) |
| A | input matrix |
| A_rows | number of rows of the input matrix |
| A_cols | number of columns of the input matrix |
| ind | vector containing computed indices, length must be A_cols if dimension == 1, or A_rows if dimension == 2 |
| work | work buffer of size >= 0 if dimension == 1, or size >= (A_rows*A_cols) if dimension == 2 |
| dimension | the dimension along which largest elements have to be computed |
Definition at line 1143 of file gmath.h.
{
const T *m_it;
int m_rows;
int m_cols;
switch(dimension)
{
case 1:
m_it = A;
m_rows = A_rows;
m_cols = A_cols;
break;
case 2:
transpose(A, A_rows, A_cols, work);
m_it = work;
m_rows = A_cols;
m_cols = A_rows;
break;
default:
throw gException(gurls::Exception_Illegal_Argument_Value);
}
for(unsigned long *r_it = ind, *r_end = ind+m_cols; r_it != r_end; ++r_it, m_it += m_rows)
*r_it = (std::max_element(m_it, m_it+m_rows) - m_it);
}
| T* gurls::lambdaguesses | ( | const T * | eigvals, |
| const int | len, | ||
| const int | r, | ||
| const int | n, | ||
| const int | nlambda, | ||
| const T | minl | ||
| ) |
| eigvals | vector containing the eigenvalues of 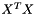 or or 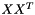 where where 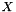 is the input data matrix is the input data matrix |
| len | number of elements of input vector |
| r | rank |
| n | number of samples |
| nlambda | |
| minl |
Definition at line 1226 of file gmath.h.
{
T* guesses = new T[nlambda];
T* tmp = new T[len];
copy(tmp, eigvals, len);
std::sort(tmp, tmp+len);
/*const*/ T lmin = tmp[len-r];
const T lmax = tmp[len-1];
delete[] tmp;
T thr1 = std::min(lmin, minl*lmax);
T thr2 = 200*static_cast<T>(sqrt(std::numeric_limits<T>::epsilon()));
lmin = std::max(thr1, thr2);
const T base = (lmax/lmin);
const T den = nlambda-static_cast<T>(1.0);
const T nT = (T)n;
for(int i=0; i< nlambda; ++i)
guesses[i] = (lmin * pow( base, ((T)i)/den ) )/nT;
return guesses;
}
| GURLS_EXPORT bool gurls::lt | ( | float | a, |
| float | b | ||
| ) |
| GURLS_EXPORT bool gurls::lt | ( | double | a, |
| double | b | ||
| ) |
| void gurls::lu | ( | gMat2D< T > & | A, |
| gVec< int > & | pv | ||
| ) |
The factorization has the form A = P * L * U where P is a permutation matrix, L is lower triangular with unit diagonal elements (lower trapezoidal if m > n), and U is upper triangular (upper trapezoidal if m < n). This is the right-looking Level 3 BLAS version of the algorithm.
| void gurls::maxValues | ( | const T * | A, |
| const int | A_rows, | ||
| const int | A_cols, | ||
| T * | maxv, | ||
| T * | work, | ||
| const int | dimension | ||
| ) | throw (gException) |
| A | input matrix |
| A_rows | number of rows of the input matrix |
| A_cols | number of columns of the input matrix |
| maxv | vector containing computed values, length must be A_cols if dimension == 1, or A_rows if dimension == 2 |
| work | work buffer of size >= 0 if dimension == 1, or size >= (A_rows*A_cols) if dimension == 2 |
| dimension | the dimension along which largest elements have to be computed |
Definition at line 1183 of file gmath.h.
{
const T *m_it;
int m_rows;
int m_cols;
switch(dimension)
{
case 1:
m_it = A;
m_rows = A_rows;
m_cols = A_cols;
break;
case 2:
transpose(A, A_rows, A_cols, work);
m_it = work;
m_rows = A_cols;
m_cols = A_rows;
break;
default:
throw gException(gurls::Exception_Illegal_Argument_Value);
}
for(T *r_it = maxv, *r_end = maxv+m_cols; r_it != r_end; ++r_it, m_it += m_rows)
*r_it = *std::max_element(m_it, m_it+m_rows);
}
| void gurls::mean | ( | const T * | A, |
| T * | result, | ||
| const int | A_rows, | ||
| const int | A_cols, | ||
| const int | res_length | ||
| ) | throw (gException) |
| A | input matrix |
| result | vecotr of length A_cols containing mean values for each row of the matrix |
| A_rows | number of rows of matrix A |
| A_cols | number of columns of matrix A |
| res_length | results vector length (MUST be == A_cols) |
| T gurls::median | ( | T * | v, |
| const int | length | ||
| ) |
| void gurls::median | ( | const T * | M, |
| const int | rows, | ||
| const int | cols, | ||
| const int | dimension, | ||
| T * | res, | ||
| T * | work | ||
| ) |
| M | input matrix |
| rows | number of rows of the input matrix |
| cols | number of columns of the input matrix |
| res | output median values vector, size == cols if dimension == 1 or size == rows if dimension == 2 |
| work | work buffer of size >= rows if dimension == 1 or >= cols if dimension == 2 |
Definition at line 1778 of file gmath.h.
{
switch(dimension)
{
case 1:
for(int i=0; i<cols; ++i)
{
copy(work, M+(i*rows), rows);
res[i] = median(work, rows);
}
break;
case 2:
for(int i=0; i<rows; ++i)
{
copy(work, M+i, cols, 1, rows);
res[i] = median(work, cols);
}
break;
default:
throw gException(Exception_Illegal_Argument_Value);
}
}
| void gurls::mldivide_squared | ( | const T * | A, |
| T * | B, | ||
| const int | a_rows, | ||
| const int | a_cols, | ||
| const int | b_rows, | ||
| const int | b_cols, | ||
| const CBLAS_TRANSPOSE | transA | ||
| ) |
| A | first input matrix |
| B | second input matrix. On exit B contains the result matrix |
| a_rows | number of rows of matrix A |
| a_cols | number of columns of matrix A |
| b_rows | number of rows of matrix B |
| b_cols | number of columns of matrix B |
| transA | specifies whether to transpose A or not |
Definition at line 1290 of file gmath.h.
{
if (a_cols != a_rows)
throw gException("The input matrix A must be squared");
const int lda = a_rows;
const int ldb = b_rows;
trsm(CblasLeft, CblasUpper, transA, CblasNonUnit, b_rows, b_cols, (T)1.0, A, lda, B, ldb);
}
| void gurls::mult | ( | const T * | A, |
| const T * | B, | ||
| T * | result, | ||
| const int | len | ||
| ) |
| GURLS_EXPORT std::ostream& gurls::operator<< | ( | std::ostream & | os, |
| const GurlsOption & | opt | ||
| ) |
Writes an option to a stream.
Definition at line 58 of file options.cpp.
{
opt.operator <<(os);
return os;
}
| void gurls::pdist | ( | const T * | A, |
| const int | N, | ||
| const int | P, | ||
| T * | D | ||
| ) |
Rows of A correspond to observations, columns correspond to variables. D is a 1-by-(N*(N-1)/2) vector, corresponding to the N*(N-1)/2 pairs of observations in A.
Definition at line 1502 of file gmath.h.
{
T* work = new T[P];
T* rowN = new T[P];
T* rowNPlusOne = new T[P];
T* D_it = D;
for(int i=0; i<N-1; ++i)
{
getRow(A, N, P, i, rowN);
for(int j=i+1; j<N; ++j)
{
getRow(A, N, P, j, rowNPlusOne);
*D_it = eucl_dist(rowN,rowNPlusOne,P, work);
++D_it;
}
}
delete [] work;
delete [] rowN;
delete [] rowNPlusOne;
}
| T* gurls::pinv | ( | const T * | A, |
| const int | rows, | ||
| const int | cols, | ||
| int & | res_rows, | ||
| int & | res_cols, | ||
| T * | RCOND = NULL |
||
| ) |
| A | input matrix |
| rows | number of rows |
| cols | number of columns |
| res_rows | on exit contains the number of rows of the pseudoinverse matrix |
| res_cols | on exit contains the number of columns of the pseudoinverse matrix |
| RCOND | used to determine the effective rank of A. If *RCOND < 0, machine precision is used |
Definition at line 423 of file gmath.h.
{
int M = rows;
int N = cols;
T* a = new T[rows*cols];
copy(a, A, rows*cols);
int LDA = M;
int LDB = std::max(M, N);
int NRHS = LDB;
const int b_size = LDB*NRHS;
T *b = new T[LDB*NRHS];
set(b, (T)0.0, b_size);
set(b, (T)1.0, std::min(LDB, NRHS), NRHS+1);
T* S = new T[std::min(M,N)];
T rcond = (RCOND == NULL)? (std::max(rows, cols)*std::numeric_limits<T>::epsilon()): *RCOND;
int RANK = -1; // std::min(M,N);
int LWORK = -1; //2 * (3*LDB + std::max( 2*std::min(M,N), LDB));
T* WORK = new T[1];
int INFO;
/* Query and allocate the optimal workspace */
gelss( &M, &N, &NRHS, a, &LDA, b, &LDB, S, &rcond, &RANK, WORK, &LWORK, &INFO);
LWORK = static_cast<int>(WORK[0]);
delete [] WORK;
WORK = new T[LWORK];
gelss( &M, &N, &NRHS, a, &LDA, b, &LDB, S, &rcond, &RANK, WORK, &LWORK, &INFO);
delete [] S;
delete [] WORK;
delete [] a;
if(INFO != 0)
{
delete [] b;
std::stringstream str;
str << "Pinv failed, error code " << INFO << ";" << std::endl;
throw gException(str.str());
}
res_rows = LDB;
res_cols = NRHS;
return b;
}
| T gurls::precrec_driver | ( | const T * | out, |
| const T * | gt, | ||
| const unsigned long | N, | ||
| T * | work | ||
| ) |
| out | vector of predicted labels |
| gt | vector of true labels |
| N | size of out and gt |
| work | Work buffer of length 4*N |
Definition at line 92 of file utils.h.
{
std::multimap<T, T, LtCompare<T> > data;
for (unsigned long i = 0; i < N; i++)
data.insert(std::pair<T,T>(-out[i], gt[i]));
typename std::multimap<T, T, LtCompare<T> >::iterator it = data.begin();
typename std::multimap<T, T, LtCompare<T> >::iterator end = data.end();
T* tp = work;
T* fp = tp+N;
T* prec = fp+N;
T* rec = prec+N;
unsigned long tpcumsum = 0;
unsigned long fpcumsum = 0;
unsigned long idx = 0;
while (it != end)
{
tp[idx] = static_cast<T>(gurls::gt(it->second, (T)0.0) ? tpcumsum+=1 : tpcumsum);
fp[idx] = static_cast<T>(gurls::lt(it->second, (T)0.0) ? fpcumsum+=1 : fpcumsum);
++it;
++idx;
}
for (idx = 0; idx < N; ++idx)
{
rec[idx] = tp[idx]/(T)tpcumsum;
prec[idx] = tp[idx]/(tp[idx]+fp[idx]);
}
// compute average precision
T ap = 0.0;
T p = 0.0;
T t = 0.0;
LtCompare<T> comp;
const int stepsNumber = 11;
const T incr = static_cast<T>(0.1);
for(int steps = 0; steps<stepsNumber; ++steps)
{
p = 0.0;
for (idx = 0; idx < N; ++idx)
{
if ( gurls::gt(rec[idx], t) || gurls::eq(rec[idx], t))
p = std::max<T, LtCompare<T> >(p, prec[idx], comp);
}
ap += p;
t += incr;
}
return ap/((T)stepsNumber);
}
| T gurls::precrec_driver | ( | const T * | out, |
| const T * | gt, | ||
| const unsigned long | N | ||
| ) |
| out | vector of predicted labels |
| gt | vector of true labels |
| N | size of out and gt |
Definition at line 162 of file utils.h.
{
T* work = new T[4*N];
T ret = precrec_driver(out, gt, N, work);
delete [] work;
return ret;
}
| void gurls::qr_econ | ( | const T * | A, |
| int | m, | ||
| int | n, | ||
| T * | Q, | ||
| T * | R, | ||
| int * | E | ||
| ) |
If m > n, only the first n columns of Q and the first n rows of R are computed.
| A | input matrix |
| m | number of rows of the input matrix |
| n | number of columns of the input matrix |
| Q | Q matrix |
| R | upper triangular R matrix |
| E | permutations vector |
Definition at line 1624 of file gmath.h.
{
// Q: mxmin(m,n)
// R: min(m,n)xn
// E: n
T* Q_tmp = new T[m*n];
copy(Q_tmp, A, m*n);
int k = std::min(m, n);
int lda = std::max(1,m);
int* jpvt = E;
set(jpvt, 0, n);
T* tau = new T[k];
T* work;
int lwork = -1;
int info;
// query
T qwork;
geqp3( &m, &n, Q_tmp, &lda, jpvt, tau, &qwork, &lwork, &info);
// exec
lwork = static_cast<int>(qwork);
work = new T[lwork];
geqp3( &m, &n, Q_tmp, &lda, jpvt, tau, work, &lwork, &info);
if(info != 0)
{
delete[] tau;
delete[] work;
delete[] Q_tmp;
std::stringstream str;
str << "QR factorization failed, error code " << info << std::endl;
throw gException(str.str());
}
if(R != NULL)
{
for(int i=0; i<n; ++i)
{
copy(R + k*i, Q_tmp + m*i, i+1);
set(R + (k*i) + i+1, (T)0.0, k - (i+1));
}
}
// query
lwork = -1;
orgqr(&m, &k, &k, Q_tmp, &lda, tau, &qwork, &lwork, &info);
if(info != 0)
{
delete[] tau;
delete[] work;
delete[] Q_tmp;
std::stringstream str;
str << "QR factorization failed, error code " << info << std::endl;
throw gException(str.str());
}
//exec
lwork = static_cast<int>(qwork);
delete[] work;
work = new T[lwork];
orgqr(&m, &k, &k, Q_tmp, &lda, tau, work, &lwork, &info);
copy(Q, Q_tmp, m*k);
delete[] tau;
delete[] work;
delete[] Q_tmp;
}
| void gurls::random_svd | ( | const T * | A, |
| const unsigned long | A_rows, | ||
| const unsigned long | A_cols, | ||
| T * | U, | ||
| T * | S, | ||
| T * | V, | ||
| unsigned long | k = 6, |
||
| unsigned long | its = 2, |
||
| unsigned long | l = 0 |
||
| ) |
| A | Matrix |
| A_rows | Number of rows of A |
| A_cols | Number of columns of A |
| U | Matrix |
| S | Matrix |
| V | Matrix |
| k | Rank, must be a positive integer <= the smallest dimension of A. |
| its | Iterations of Lanczos method |
| l | Block size |
Definition at line 520 of file utils.h.
{
// U: (A_rows,k)
// S: (k)
// V: (A_cols, k)
if(l < k)
l = k+2;
if((k > A_rows) || (k > A_cols))
throw gException("k must be <= the smallest dimension of A");
// %
// % SVD A directly if (its+1)*l >= m/1.25 or (its+1)*l >= n/1.25.
// %
// if(((its+1)*l >= m/1.25) || ((its+1)*l >= n/1.25))
const T thr1 = static_cast<T>(A_rows/1.25);
const T thr2 = static_cast<T>(A_cols/1.25);
const T block_dim = static_cast<T>((its+1)*l);
if(gt(block_dim, thr1) || eq(block_dim, thr1) || gt(block_dim, thr2) || eq(block_dim, thr2))
{
// [U,S,V] = svd(A,'econ');
T *Q, *L, *Vt;
int Q_rows, Q_cols;
int L_len;
int Vt_rows, Vt_cols;
svd(A, Q, L, Vt, A_rows, A_cols, Q_rows, Q_cols, L_len, Vt_rows, Vt_cols, true);
// %
// % Retain only the leftmost k columns of U, the leftmost k columns of V,
// % and the uppermost leftmost k x k block of S.
// %
// U = U(:,1:k);
copy(U, Q, k*Q_rows);
delete[] Q;
// S = S(1:k,1:k);
copy(S, L, k);
delete[] L;
// V = V(:,1:k);
if(V != NULL)
{
T* tr = new T[Vt_cols*Vt_rows];
transpose(Vt, Vt_rows, Vt_cols, tr);
copy(V, tr, k*Vt_cols);
delete[] tr;
}
delete[] Vt;
return;
}
const T randMax = static_cast<T>(RAND_MAX);
const T one = static_cast<T>(1.0);
const T two = static_cast<T>(2.0);
// if(m >= n)
if(A_rows >= A_cols)
{
const int H_len = A_rows*l;
T* H = new T[H_len];
T* tmp = new T[A_cols*l];
// %
// % Apply A to a random matrix, obtaining H.
// %
// H = A*(2*rand(n,l)-ones(n,l));
for(T *it =tmp, *end = tmp +(A_cols*l); it != end; ++it)
*it = (two* rand()/randMax) - one;
dot(A, tmp, H, A_rows, A_cols, A_cols, l, A_rows, l, CblasNoTrans, CblasNoTrans, CblasColMajor);
// %
// % Initialize F to its final size and fill its leftmost block with H.
// %
// F(1:m, 1:l) = H;
const unsigned long F_cols = static_cast<unsigned long>(block_dim);
T* F = new T[A_rows*F_cols];
copy(F, H, H_len);
// %
// % Apply A*A' to H a total of its times,
// % augmenting F with the new H each time.
// %
// for it = 1:its
for(unsigned long iter = 1; iter<=its; ++iter)
{
// H = (H'*A)';
// H = A*H;
dot(H, A, tmp, A_rows, l, A_rows, A_cols, l, A_cols, CblasTrans, CblasNoTrans, CblasColMajor);
dot(A, tmp, H, A_rows, A_cols, l, A_cols, A_rows, l, CblasNoTrans, CblasTrans, CblasColMajor);
// F(1:m, (1+it*l):((it+1)*l)) = H;
copy(F + (H_len*iter), H, H_len);
}
delete[] H;
// %
// % Form a matrix Q whose columns constitute an orthonormal basis
// % for the columns of F.
// %
// [Q,R,E] = qr(F,0);
const unsigned long Q_cols = std::min(A_rows, F_cols);
T* Q = new T[A_rows*Q_cols];
T* R = NULL;
int* E = new int [F_cols];
qr_econ(F, A_rows, F_cols, Q, R, E);
delete[] E;
delete[] F;
// %
// % SVD Q'*A to obtain approximations to the singular values
// % and right singular vectors of A; adjust the left singular vectors
// % of Q'*A to approximate the left singular vectors of A.
// %
// [U2,S,V] = svd(Q'*A,'econ');
T *U2, *L, *Vt;
int U2_rows, U2_cols;
int L_len;
int Vt_rows, Vt_cols;
delete[] tmp;
tmp = new T[Q_cols*A_cols];
dot(Q, A, tmp, A_rows, Q_cols, A_rows, A_cols, Q_cols, A_cols, CblasTrans, CblasNoTrans, CblasColMajor);
svd(tmp , U2, L, Vt, Q_cols, A_cols, U2_rows, U2_cols, L_len, Vt_rows, Vt_cols, true);
// U = Q*U2;
delete[] tmp;
tmp = new T[A_rows*U2_cols];
dot(Q, U2, tmp, A_rows, Q_cols, U2_rows, U2_cols, A_rows, U2_cols, CblasNoTrans, CblasNoTrans, CblasColMajor);
// clear Q U2;
delete[] Q;
delete[] U2;
// %
// % Retain only the leftmost k columns of U, the leftmost k columns of V,
// % and the uppermost leftmost k x k block of S.
// %
// U = U(:,1:k);
copy(U, tmp, k*A_rows);
delete[] tmp;
// V = V(:,1:k);
if(V != NULL)
{
T* tr = new T[Vt_cols*Vt_rows];
transpose(Vt, Vt_rows, Vt_cols, tr);
copy(V, tr, k*Vt_cols);
delete[] tr;
}
delete[] Vt;
// S = S(1:k,1:k);
copy(S, L, k);
delete[] L;
}
else
{
// %
// % Apply A' to a random matrix, obtaining H.
// %
const int H_len = A_cols*l;
// H = ((2*rand(l,m)-ones(l,m))*A)';
T* H = new T[H_len];
T* tmp = new T[l*A_rows];
for(T *it =tmp, *end = tmp +(l*A_rows); it != end; ++it)
*it = (two* rand()/randMax) - one;
dot(A, tmp, H, A_rows, A_cols, l, A_rows, A_cols, l, CblasTrans, CblasTrans, CblasColMajor);
// %
// % Initialize F to its final size and fill its leftmost block with H.
// %
// F = zeros(n,(its+1)*l);
// F(1:n, 1:l) = H;
const unsigned long F_cols = static_cast<unsigned long>(block_dim);
T* F = new T[A_cols*F_cols];
copy(F, H, H_len);
// %
// % Apply A'*A to H a total of its times,
// % augmenting F with the new H each time.
// %
// for it = 1:its
for(unsigned long iter = 1; iter<=its; ++iter)
{
// H = A*H;
dot(A, H, tmp, A_rows, A_cols, A_cols, l, A_rows, l, CblasNoTrans, CblasNoTrans, CblasColMajor);
// H = (H'*A)';
dot(A, tmp, H, A_rows, A_cols, A_rows, l, A_cols, l, CblasTrans, CblasNoTrans, CblasColMajor);
// F(1:n, (1+it*l):((it+1)*l)) = H;
copy(F + (H_len*iter), H, H_len);
}
delete[] H;
// %
// % Form a matrix Q whose columns constitute an orthonormal basis
// % for the columns of F.
// %
// [Q,R,E] = qr(F,0);
const unsigned long Q_cols = std::min(A_cols, F_cols);
T* Q = new T[A_cols*Q_cols];
T* R = NULL;
int* E = new int [F_cols];
qr_econ(F, A_cols, F_cols, Q, R, E);
delete[] E;
delete[] F;
// %
// % SVD A*Q to obtain approximations to the singular values
// % and left singular vectors of A; adjust the right singular vectors
// % of A*Q to approximate the right singular vectors of A.
// %
// [U,S,V2] = svd(A*Q,'econ');
T *U2, *L, *Vt;
int U2_rows, U2_cols;
int L_len;
int Vt_rows, Vt_cols;
delete[] tmp;
tmp = new T[A_rows*Q_cols];
dot(A, Q, tmp, A_rows, A_cols, A_cols, Q_cols, A_rows, Q_cols, CblasNoTrans, CblasNoTrans, CblasColMajor);
svd(tmp, U2, L, Vt, A_rows, Q_cols, U2_rows, U2_cols, L_len, Vt_rows, Vt_cols, true);
// V = Q*V2;
delete[] tmp;
if(V != NULL)
{
tmp = new T[A_cols*Vt_rows];
dot(Q, Vt, tmp, A_cols, Q_cols, Vt_rows, Vt_cols, A_cols, Vt_rows, CblasNoTrans, CblasTrans, CblasColMajor);
}
delete[] Vt;
delete[] Q;
// %
// % Retain only the leftmost k columns of U, the leftmost k columns of V,
// % and the uppermost leftmost k x k block of S.
// %
// U = U(:,1:k);
copy(U, U2, k*U2_rows);
delete[] U2;
// V = V(:,1:k);
if(V != NULL)
copy(V, tmp, k*A_cols);
delete[] tmp;
// S = S(1:k,1:k);
copy(S, L, k);
delete[] L;
}
}
| void gurls::rdivide | ( | const T * | A, |
| const T * | B, | ||
| T * | result, | ||
| const int | len | ||
| ) |
| void gurls::rls_eigen | ( | const T * | Q, |
| const T * | L, | ||
| const T * | Qty, | ||
| T * | C, | ||
| const T | lambda, | ||
| const int | n, | ||
| const int | Q_rows, | ||
| const int | Q_cols, | ||
| const int | L_length, | ||
| const int | Qty_rows, | ||
| const int | Qty_cols | ||
| ) |
| Q | eigenvectors of the kernel matrix |
| L | eigenvalues of the kernel matrix |
| Qty | result of the matrix multiplication of the transpose of Q times the labels vector Y 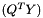 |
| C | on exit contains the rls coefficients matrix |
| lambda | regularization parameter |
| n | number of training samples |
| Q_rows | number of rows of the matrix Q |
| Q_cols | number of columns of the matrix Q |
| L_length | number of elements of the vector L |
| Qty_rows | number of rows of the matrix Qty |
| Qty_cols | number of columns of the matrix Qty |
Definition at line 940 of file gmath.h.
{
T* work = new T [(Q_rows+1)*L_length];
rls_eigen(Q, L, Qty, C, lambda, n, Q_rows, Q_cols, L_length, Qty_rows, Qty_cols, work);
delete [] work;
}
| void gurls::rls_eigen | ( | const T * | Q, |
| const T * | L, | ||
| const T * | Qty, | ||
| T * | C, | ||
| const T | lambda, | ||
| const int | n, | ||
| const int | Q_rows, | ||
| const int | Q_cols, | ||
| const int | L_length, | ||
| const int | Qty_rows, | ||
| const int | Qty_cols, | ||
| T * | work | ||
| ) |
| Q | eigenvectors of the kernel matrix |
| L | eigenvalues of the kernel matrix |
| Qty | result of the matrix multiplication of the transpose of Q times the labels vector Y 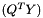 |
| C | on exit contains the rls coefficients matrix |
| lambda | regularization parameter |
| n | number of training samples |
| Q_rows | number of rows of the matrix Q |
| Q_cols | number of columns of the matrix Q |
| L_length | number of elements of the vector L |
| Qty_rows | number of rows of the matrix Qty |
| Qty_cols | number of columns of the matrix Qty |
| work | Work buffer of length L_length*(Q_rows+1) |
Definition at line 969 of file gmath.h.
{
//function C = rls_eigen(Q,L,QtY,lambda,n)
//sQ = size(Q,1); -> Q_rows
//L = L + n*lambda;
T* L1 = work; // size L_length
set(L1, n*lambda , L_length);
axpy(L_length, (T)1.0, L, 1, L1, 1);
//L = L.^(-1);
setReciprocal(L1, L_length);
// L = diag(L)
T* QL = work+L_length; // size Q_rows*L_length
copy(QL, Q, Q_rows*Q_cols);
for(int i=0; i< Q_cols; ++i)
scal(Q_rows, L1[i], QL+(Q_rows*i), 1);
//C = (Q*L)*QtY;
dot(QL, Qty, C, Q_rows, L_length, Qty_rows, Qty_cols, Q_rows, Qty_cols, CblasNoTrans, CblasNoTrans, CblasColMajor);
}
| GurlsOptionsList* gurls::rls_pegasos_driver | ( | const T * | X, |
| const T * | bY, | ||
| const GurlsOptionsList & | opt, | ||
| const int | X_rows, | ||
| const int | X_cols, | ||
| const int | bY_rows, | ||
| const int | bY_cols | ||
| ) |
| X | input data matrix |
| bY | labels matrix |
| opt | options |
| X_rows | number of rows in X |
| X_cols | number of columns in X |
| bY_rows | number of rows in bY |
| bY_cols | number of columns in bY |
Definition at line 192 of file utils.h.
{
// lambda = opt.singlelambda(opt.paramsel.lambdas);
const gMat2D<T> &ll = opt.getOptValue<OptMatrix<gMat2D<T> > >("paramsel.lambdas");
T lambda = opt.getOptAs<OptFunction>("singlelambda")->getValue(ll.getData(), ll.getSize());
// [n,d] = size(X);
const int n = X_rows;
const int d = X_cols;
// [T] = size(bY,2);
const int t = bY_cols;
// cfr = opt.cfr;
// W = cfr.W; %dxT
const GurlsOptionsList* optimizer = opt.getOptAs<GurlsOptionsList>("optimizer");
const gMat2D<T> &W_mat = optimizer->getOptValue<OptMatrix<gMat2D<T> > >("W");
gMat2D<T> *W = new gMat2D<T>(W_mat.rows(), W_mat.cols());
copy(W->getData(), W_mat.getData(), W_mat.getSize());
// W_sum = cfr.W_sum;
const gMat2D<T> &W_sum_mat = optimizer->getOptValue<OptMatrix<gMat2D<T> > >("W_sum");
gMat2D<T> *W_sum = new gMat2D<T>(W_sum_mat.rows(), W_sum_mat.cols());
copy(W_sum->getData(), W_sum_mat.getData(), W_sum_mat.getSize());
// count = cfr.count;
int count = static_cast<int>(optimizer->getOptAsNumber("count"));
// t0 = cfr.t0;
T t0 = static_cast<T>(optimizer->getOptAsNumber("t0"));
unsigned long * seq = new unsigned long[n];
T* xt = new T[d];
T* y_hat = new T[t];
T* r = new T[t];
const int W_size = d*t;
T* xtr = new T[W_size];
// %% Initialization
// iter = 0;
int iter;
const T thr = sqrt(t/lambda);
// seq = randperm(n);
randperm(n, seq);
for(iter = 0; iter<n; ++iter)
{
// while iter < n,
// iter = iter + 1;
// idx = seq(iter);
const unsigned long idx = seq[iter];
// %% Stepsize
// %% Update Equations
// xt = X(idx,:); %1xd
getRow(X, n, d, idx, xt);
// y_hat = (xt*W); %1xT
dot(xt, W->getData(), y_hat, 1, d, d, t, 1, t, CblasNoTrans, CblasNoTrans, CblasColMajor);
// r = bY(idx,:) - y_hat; %1xT
getRow(bY, bY_rows, t, idx, r);
axpy(t, (T)-1.0, y_hat, 1, r, 1);
// eta = 1.0/(lambda*(count + t0));
const T eta = ((T)1.0)/(lambda*(count + t0));
// W = (1 - lambda*eta)*W + eta*xt'*r; %dxT
const T coeff = (T)1.0 - (lambda*eta);
scal(W_size, coeff, W->getData(), 1);
dot(xt, r, xtr, d, 1, 1, t, d, t, CblasNoTrans, CblasNoTrans, CblasColMajor);
axpy(W_size, eta, xtr, 1, W->getData(), 1);
// %% Projection onto the ball with radius sqrt(T/lambda)
// nW = norm(W,'fro'); %Frobenius norm
T tmp = dot(W_size, W->getData(), 1, W->getData(), 1);
T nW = sqrt(tmp);
// if nW > sqrt(T/lambda)
if( gt(nW, thr) )
{
// W = (W/nW)*sqrt(T/lambda);
set(xtr, (T)0.0, W_size);
axpy(W_size, thr/nW, W->getData(), 1, xtr, 1);
copy(W->getData(), xtr, W_size);
}
// %% Averaging
// W_sum = W_sum + W;
axpy(W_size, (T)1.0, W->getData(), 1, W_sum->getData(), 1);
// count = count + 1;
++count;
// %% Testing
// if(mod(count,n) == 1)
// fprintf('\n\tObjective : %f',obj_primal(W, X, bY, lambda));
// cfr.acc_last(end+1) = test_classifier (W,opt);
// fprintf('\n\tLast Acc: %f', cfr.acc_last(end));
// cfr.acc_avg(end+1) = test_classifier (W_sum/count,opt);
// fprintf('\n\tAvg Acc: %f\n', cfr.acc_avg(end));
// end
}
delete[] seq;
delete[] xt;
delete[] y_hat;
delete[] r;
delete[] xtr;
GurlsOptionsList* ret = new GurlsOptionsList("optimizer");
// cfr.W = W;
ret->addOpt("W", new OptMatrix<gMat2D<T> >(*W));
// cfr.W_last = W;
// cfr.W_sum = W_sum;
ret->addOpt("W_sum", new OptMatrix<gMat2D<T> >(*W_sum));
// cfr.count = count;
ret->addOpt("count", new OptNumber(count));
// cfr.iter = iter;
ret->addOpt("iter", new OptNumber(iter));
ret->addOpt("t0", new OptNumber(t0));
// cfr.C = [];
gMat2D<T>* emptyC = new gMat2D<T>();
ret->addOpt("C", new OptMatrix<gMat2D<T> >(*emptyC));
// cfr.X = [];
gMat2D<T>* emptyX = new gMat2D<T>();
ret->addOpt("X", new OptMatrix<gMat2D<T> >(*emptyX));
return ret;
}
| void gurls::set | ( | T * | buffer, |
| const T | value, | ||
| const int | size, | ||
| const int | incr | ||
| ) |
| buffer | vector to be set |
| value | value to set |
| size | number of copy operations to be performed |
| incr | number of element to skip after every copy (if incr == 1 all elements will be set) |
| void gurls::set | ( | T * | buffer, |
| const T | value, | ||
| const int | size | ||
| ) |
| void gurls::setReciprocal | ( | T * | matrix, |
| const int | len | ||
| ) |
| T* gurls::sign | ( | const T * | vector, |
| const int | size | ||
| ) |
| vector | input vector |
| size | number of elements of the input vector |
Definition at line 1010 of file gmath.h.
{
const T* v_it = vector;
const T* v_end = vector+size;
T* ret = new T[size];
T* r_it = ret;
const T zero = (T)0.0;
while(v_it != v_end)
{
*r_it = static_cast<T>((eq(*v_it, zero)? 0.0 : ((*v_it > 0.0)? 1.0 : -1.0)));
++v_it;
++r_it;
}
return ret;
}
| void gurls::sort | ( | const T * | M, |
| const unsigned long | rows, | ||
| const unsigned long | cols, | ||
| bool(*)(T, T) | pred, | ||
| T * | values, | ||
| unsigned long * | indices | ||
| ) |
| M | Input matrix |
| rows | Matrix rows |
| cols | Matrix columns |
| pred | Binary predicate used for comparison |
| values | On ouptut contains the ordered values matrix |
| indices | On ouptut contains the ordered indices matrix |
Definition at line 1102 of file gmath.h.
{
typedef std::multimap<T, unsigned long, bool(*)(T,T) > MapType;
for(unsigned long i=0; i< rows; ++i)
{
MapType data(pred);
for (unsigned long j = 0; j < cols; ++j)
{
const unsigned long index = i+(rows*j);
data.insert( std::pair<T,unsigned long>(M[index], j));
}
typename MapType::iterator it = data.begin();
for (unsigned long j = 0; j < cols; ++j, ++it)
{
const unsigned long index = i+(rows*j);
if(values != NULL)
values[index] = it->first;
if(indices != NULL)
indices[index] = it->second;
}
}
}
| void gurls::squareform | ( | const T * | A, |
| const int | N, | ||
| const int | P, | ||
| T * | D, | ||
| const int | d_cols | ||
| ) |
If A is a vector as created by the pdist function, converts A into a symmetric, square format, so that D(i,j) denotes the distance between the i and j objects in the original data. If A is a symmetric, square matrix with zeros along the diagonal, creates a vector D containing the A elements below the diagonal. D has the same format as the output from the PDIST function.
Definition at line 1538 of file gmath.h.
{
if(d_cols!=1)
{
T* work = new T[P];
T* rowN = new T[P];
T* rowNPlusOne = new T[P];
set(D, (T)0.0, N, N+1); // zeroes the diagonal
for(int i=0; i<N; ++i)
{
copy(D+(i*N), D+i, i, 1, N); // copy from the other side
if(i+1 < N)
{
getRow(A, N, P, i, rowN);
for(int j=i+1; j<N; ++j)
{
getRow(A, N, P, j, rowNPlusOne);
D[j + i*N] = eucl_dist(rowN, rowNPlusOne, P, work);
}
}
}
delete [] work;
delete [] rowN;
delete [] rowNPlusOne;
}
else
{
pdist(A, N, P, D);
}
}
| void gurls::stdDev | ( | const T * | X, |
| const int | rows, | ||
| const int | cols, | ||
| T * | res, | ||
| T * | work | ||
| ) |
| X | input matrix |
| rows | number of rows of the input matrix |
| cols | number of columns of the input matrix |
| res | output standard deviations vector |
| work | work buffer of size >= cols+rows |
| void gurls::subMatrixFromColumns | ( | const T * | matrix, |
| const int | mRows, | ||
| const int | mCols, | ||
| const unsigned long * | colsIndices, | ||
| const int | nIndices, | ||
| T * | submat | ||
| ) |
| matrix | input matrix |
| mRows | number of rows of the input matrix |
| mCols | number of columns of the input matrix |
| colsIndices | vector containing the columns indices to copy |
| nIndices | length of the indices vector |
| submat | output submatrix |
Definition at line 374 of file gmath.h.
{
if(mCols < nIndices)
throw gException(Exception_Inconsistent_Size);
for(const unsigned long *it = colsIndices, *end = colsIndices+nIndices; it != end; ++it)
copy(submat+(mRows*(it-colsIndices)), matrix+(mRows*(*it)), mRows);
}
| void gurls::subMatrixFromRows | ( | const T * | matrix, |
| const int | mRows, | ||
| const int | mCols, | ||
| const unsigned long * | rowsIndices, | ||
| const int | nIndices, | ||
| T * | submat | ||
| ) |
| matrix | input matrix |
| mRows | number of rows of the input matrix |
| mCols | number of columns of the input matrix |
| rowsIndices | vector containing the row indices to copy |
| nIndices | length of the indices vector |
| submat | output submatrix |
Definition at line 353 of file gmath.h.
{
if(mRows < nIndices)
throw gException(Exception_Inconsistent_Size);
for(const unsigned long *it = rowsIndices, *end = rowsIndices+nIndices; it != end; ++it)
copy(submat + (it-rowsIndices), matrix+(*it), mCols, nIndices, mRows);
}
| void gurls::sum | ( | const T * | A, |
| T * | result, | ||
| const int | A_rows, | ||
| const int | A_cols, | ||
| const int | res_length | ||
| ) | throw (gException) |
| A | input matrix |
| result | vecotr of length A_cols containing sums for each row of the matrix |
| A_rows | number of rows of matrix A |
| A_cols | number of columns of matrix A |
| res_length | results vector length (MUST be == A_cols) |
Definition at line 801 of file gmath.h.
{
if(A_cols != res_length)
throw gException(Exception_Inconsistent_Size);
const T *a_it = A, *a_end;
const T zero = static_cast<T>(0.0);
for(T *r_it = result, *r_end = result+A_cols; r_it != r_end; ++r_it)
{
*r_it = zero;
a_end = a_it+A_rows;
while(a_it != a_end)
{
*r_it += *a_it;
++a_it;
}
}
}
| void gurls::sum_col | ( | const T * | A, |
| T * | result, | ||
| const int | A_rows, | ||
| const int | A_cols | ||
| ) | throw (gException) |
| A | input matrix |
| result | vecotr of length A_rows containing sums for each column of the matrix |
| A_rows | number of rows of matrix A |
| A_cols | number of columns of matrix A |
Definition at line 833 of file gmath.h.
{
const T *a_it = A, *a_end;
const T zero = static_cast<T>(0.0);
for(T *r_it = result, *r_end = result+A_rows; r_it != r_end; ++r_it)
{
*r_it = zero;
for(a_it = A+(r_it-result), a_end = a_it+(A_cols*A_rows); a_it != a_end; a_it += A_rows)
*r_it += *a_it;
}
}
| T gurls::sumv | ( | const T * | V, |
| const int | len | ||
| ) | throw (gException) |
| void gurls::svd | ( | const gMat2D< T > & | A, |
| gMat2D< T > & | U, | ||
| gVec< T > & | W, | ||
| gMat2D< T > & | Vt | ||
| ) |
| A | Matrix to be decomposed |
| U | Matrix of the left singular vectors |
| W | Vector containing the singular values of the decomposition |
| Vt | transposed matrix of the right singular vectors |
| void gurls::svd | ( | const T * | A, |
| T *& | U, | ||
| T *& | S, | ||
| T *& | Vt, | ||
| const int | A_rows, | ||
| const int | A_cols, | ||
| int & | U_rows, | ||
| int & | U_cols, | ||
| int & | S_len, | ||
| int & | Vt_rows, | ||
| int & | Vt_cols, | ||
| bool | econ = false |
||
| ) | throw (gException) |
| A | Input matrix to be decomposed |
| U | Matrix of the left singular vectors |
| S | Vector containing the singular values of the decomposition |
| Vt | transposed matrix of the right singular vectors |
| A_rows | number of rows of matrix A |
| A_cols | number of columns of matrix A |
| U_rows | number of rows of matrix U |
| U_cols | number of columns of matrix U |
| S_len | number of elements of vector S |
| Vt_rows | number of rows of matrix Vt |
| Vt_cols | number of columns of matrix Vt |
| econ | if true computes the "economy size" decomposition. If A_rows >= A_cols, then svd computes only the first A_cols columns of U and S length is A_cols. For A_rows < A_cols, only the first A_rows rows of Vt are computed and S length is A_rows. |
Definition at line 1324 of file gmath.h.
{
// A = U*S*Vt
char jobu, jobvt;
int m = A_rows;
int n = A_cols;
int k = std::min<int>(m, n);
int ldvt;
S = new T[k];
S_len = k;
U_rows = m;
Vt_cols = n;
if(econ)
{
// jobu = jobvt = 'S';
if(m>n)
{
jobu = 'S';
jobvt = 'A';
}
else if(m<n)
{
jobu = 'A';
jobvt = 'S';
}
else
jobu = jobvt = 'S';
U = new T[m*k];
Vt = new T[k*n];
U_cols = k;
Vt_rows = k;
ldvt = k;
}
else
{
jobu = jobvt = 'A';
U = new T[m*m];
Vt = new T[n*n];
U_cols = m;
Vt_rows = n;
ldvt = n;
}
//MAX(1,3*MIN(M,N)+MAX(M,N),5*MIN(M,N))
int lda = A_rows;
int ldu = m;
int info, lwork = std::max<int>(3*k+std::max<int>(m,n), 5*k);
T* work = new T[lwork];
T* cpy = new T[m*n];
copy(cpy, A, A_rows*A_cols);
gesvd_(&jobu, &jobvt, &m, &n, cpy, &lda, S, U, &ldu, Vt, &ldvt, work, &lwork, &info);
delete[] work;
delete[] cpy;
if(info != 0)
{
std::stringstream str;
str << "SVD failed, error code " << info << std::endl;
throw gException(str.str());
}
}
| static const std::string gurls::TASKDESC_SEPARATOR | ( | ":" | ) | [static] |
"<task_desc>TASKDESC_SEPARATOR<task_name>")
| T gurls::test_classifier | ( | T * | W, |
| GurlsOptionsList & | opt, | ||
| const int | rows, | ||
| const int | cols | ||
| ) |
| W | coefficient vector for a linear classifier |
| opt | options with the followng fields:
|
| rows | number of rows in W |
| cols | number of columns in W |
Definition at line 365 of file utils.h.
{
//opt.rls.W = W;
GurlsOptionsList* optimizer = GurlsOptionsList::dynacast(opt.getOpt("optimizer"));
gMat2D<T> *W_mat = NULL;
if(!optimizer->hasOpt("W"))
{
W_mat = new gMat2D<T>(rows,cols);
optimizer->addOpt("W", new OptMatrix<gMat2D<T> >(*W_mat));
}
else
{
GurlsOption *W_opt = optimizer->getOpt("W");
W_mat = &(OptMatrix<gMat2D<T> >::dynacast(W_opt))->getValue();
}
gMat2D<T> W_t(W, W_mat->cols(), W_mat->rows(), false);
W_t.transpose(*W_mat);
GurlsOption *x = opt.getOpt("Xte");
gMat2D<T>* X = &(OptMatrix< gMat2D<T> >::dynacast(x))->getValue();
GurlsOption *y = opt.getOpt("yte");
gMat2D<T>* Y = &(OptMatrix< gMat2D<T> >::dynacast(y))->getValue();
//opt.pred = pred_primal(opt.Xte, opt.yte, opt);
PredPrimal<T> pp;
pp.execute(*X, *Y, opt);
//opt.perf = perf_macroavg(opt.Xte, opt.yte, opt);
PerfMacroAvg<T> ma;
ma.execute(*X, *Y, opt);
//acc = mean([opt.perf.acc]);
GurlsOptionsList* perf = GurlsOptionsList::dynacast(opt.getOpt("perf"));
GurlsOption *perf_opt = perf->getOpt("acc");
gMat2D<T> *acc_mat = &(OptMatrix<gMat2D<T> >::dynacast(perf_opt))->getValue();
T res;
mean<T>(acc_mat->getData(), &res, 1, acc_mat->getSize(), 1);
return res;
}
| void gurls::transpose | ( | const T * | matrix, |
| const int | rows, | ||
| const int | cols, | ||
| T * | transposed | ||
| ) |
| matrix | input matrix to be transposed |
| rows | number of rows of the input matrix |
| cols | number of columns of the input matrix |
| transposed | on exit contains the transposed matrix. Must be already initialized with a number of rows and columns equal to the number of columns and rows of the input matrix |
Definition at line 487 of file gmath.h.
{
T* d1 = transposed;
const T* d0 = matrix;
const int N = rows;
for (int r = 0; r < rows; ++r)
for (int c = 0; c < cols; ++c)
*d1++=*(d0+c*N+r);
}
const int gurls::MAX_PRINTABLE_SIZE = 200 [static] |
Verctor with a largest size will not be printed out
Definition at line 64 of file basearray.h.